3 アルゴリズム

3.1 単純挿入ソート

3.1.1 単純挿入ソートの考え方

単純挿入ソートは，a[0]からa[i-1]まで並び替えが終わって いるとき，a[i]を正しい位置に入れる--ことを繰り返す方法である．その様子を図 20に示す．処理の手順は次の通りである．

1. 処理するa[i]の値35よりも，48は大きいので35の場所へ移動させる．
2. 次の44も35より大きいので，48の場所へ移動させる．
3. 次の41も35より大きいので，44の場所へ移動させる．
4. 次の39も35より大きいので，41の場所へ移動させる．
5. 次の32は35より小さいので，それは移動させない．そして，元の35を39の場所へ 移動させる．

図 20: 単純挿入ソートの基本操作．a[i]を正しい位置に入れる．

3.1.2 プログラム

単純挿入ソートの実際のプログラム(関数)は，教科書 [1]p.219のリスト 6.20のように書く．整列させる整数のデータは，配列はarray[]に格納されている． データの個数はnumに格納されている．したがって，整列すべき整数のデータは，配 列のarray[0]〜array[num-1]に格納されている．

この関数がソートする様子を図21に示す．先に示したアルゴリズ ムの通りであることが分かるだろう．

この関数を呼び出すときには，次のようにする．

	insertion_sort(a,10);

整列すべき整数は，a[0]〜a[9]に入っている．データの個数は10個である．

著作権の関係で，教科書のこのプログラムはここには書かないが，よく理解しておけ!

図 21: 単純挿入ソートを使った整数の整列．教科書 [1]p.219のリスト 6.20 insertion_sort()関数の動作．

3.1.3 計算量

単純挿入ソートの計算量は，内側の繰り返し分のループ回数で決まる．教科書 []p.219のリスト6.20では，jの部分のループ回数である．ここでは，その計算 量のオーダーを見積もる．

ソートするデータの個数を$N$とする．外側のループは$i=1$〜$N-1$までである．データがランダムの場合， 内側のループは平均して$i/2$回繰り返される．したがって，内側のループの総繰り返し回数は，

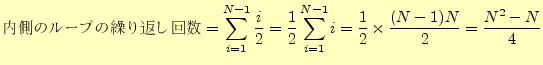$$\texttt{内側のループの繰り返し回数} =\sum_{i=1}^{N-1}\frac{i}{2} =\frac{1}{2}\sum_{i=1}^{N-1}i =\frac{1}{2}\times\frac{(N-1)N}{2} =\frac{N^2-N}{4}$$ (1)

となる．データの個数が大きくなると，$N^2$が支配的になる．したがって，計算量のオー ダーは$O(N^2)$となる．コンピューターでの処理の時間は，データ数の二乗($N^2$)で増 加するということである．

ホームページ: Yamamoto's laboratory
著者: 山本昌志