2 実数の関数
2.1 数学関数の例
C言語では,ヘッダーファイルmath.hをインクルードすることにより,おなじみの数 学の初等関数を使うことができる.具体的には,リスト1のようにする. 1 #include <stdio.h>
2 #include <math.h>
3
4 int main(void){
5 double x, s, c, t, l, e;
6
7 x=M_PI;
8
9 s=sin(x);
10 c=cos(x);
11 e=exp(x);
12 l=log(x);
13
14 printf("sin(pi)=%f\n",s);
15 printf("cos(pi)=%f\n",c);
16 printf("tan(pi)=%f\n",t);
17 printf("exp(pi)=%f\n",e);
18 printf("log(pi)=%f\n",l);
19
20 return 0;
21 }
sin(pi)=0.000000 cos(pi)=-1.000000 tan(pi)=0.000000 exp(pi)=23.140693 log(pi)=1.144730
このプログラムの各行の内容は,次の通りである.
- 2行目 #include <math.h>
数学関数を使うために,ヘッダーファイルmath.h をインクルードしている.数学 関数を使う場合,必ず必要である.
- 7行目 x=M_PI;
M_PIは円周率を表すマクロである.math.hをインクルードすると, M_PIはコンパイル時に,
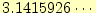 に置き換わる.
に置き換わる.
- 9-12行目 s=sin(x);など
おなじみの数学関数が並んでいる.右辺の関数の戻り値を左辺の変数に代入している.
2.2 数学関数の使用方法
2.2.1 記述方法
数学関数を使うためには,math.hをインクルードすることを忘れてはならない.ま ずは,これを書く.C言語の数学関数は,数学で使う初等関数とほとんど同じ記述のため簡単である.必要な関数 を数学で学習したように記述すればよい.math.hに用意されている関数は,表 1のとおである.引数も戻り値も倍精度実数型である.
数学の計算でしばしば使われる定数は,math.hでマクロとして定義されている.定 義されているマクロを表2に示す.いろいろ定義されているが, 円周率を表すM_PIを憶えておけば,ほとんどの場合事足りる.次に重要なのは,ネ ピア数を表すM_Eくらいである.
2.2.2 コンパイル方法
数学関数を含んだソースファイルをコンパイルする場合には,libmというライブラ リーをリンクする必要がある.このライブラリーが数学関数の実体である.数学関数が使 われているときには,gcc -o fugafuga hogehoge.c -lm
のようにする.hogehoge.cがソースファイルで,fugafugaが実行ファイルであ る.オプション-lmをつけることにより,数学関数のライブラリーlibmをリン クしている.
| 数学関数名 | C言語関数 | 引数x | 戻り値 |
| 三角関数 | sin(x) | 単位はラジアン | |
| cos(x) | 単位はラジアン | ||
| tan(x) | 単位はラジアン | ||
| 逆三角関数 | asin(x) | 範囲 |
範囲
|
| acos(x) | 範囲 |
範囲 |
|
| atan(x) | 範囲
|
||
| atan2(x,y) |
|
||
| 双曲線関数 | sinh(x) | ||
| cosh(x) | |||
| tanh(x) | |||
| 指数関数 | exp(x) | ||
| 対数 | log(x) | 0 |
自然対数 |
| log10(x) | 0 |
常用対数
|
|
| 絶対値 | fabs(x) | ||
| 平方根 | sqrt(x) | ||
| べき乗 | pow(x,y) | xもyも実数可 | |
| 整数部 | floor(x) | ||
| ceil(x) |
| 数学定数名 | 数学記号 | C言語マクロ | 値 |
| 円周率 | M_PI | 3.14159265358979323846 | |
| M_PI_2 | 1.57079632679489661923 | ||
| M_PI_4 | 0.78539816339744830962 | ||
| M_1_PI | 0.31830988618379067154 | ||
| M_2_PI | 0.63661977236758134308 | ||
|
|
M_2_SQRTPI | 1.12837916709551257390 | |
| ネピア数 | M_E | 2.7182818284590452354 | |
| M_LOG2E | 1.4426950408889634074 | ||
|
|
M_LOG10E | 0.43429448190325182765 | |
| 対数 | M_LN2 | 0.69314718055994530942 | |
| M_LN10 | 2.30258509299404568402 | ||
| 平方根 | M_SQRT2 | 1.41421356237309504880 | |
|
|
M_SQRT1_2 | 0.70710678118654752440 |
2.3 練習問題
- [練習1]
- キーボードより変数の値を読み込み,以下の関数の値を表示せよ.
- 三角関数(
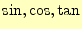 )
)
- 指数関数
- 自然対数関数と常用対数関数
- 平方根と立方根
- 三角関数(
- [練習2]
- キーボードより変数の値を読み込んで,sqrt(x)と pow(x,0.5)の関数の値を比較せよ.
- [練習3]
- math.hで定義されたマクロ定数を用いて,円周率
 とネピア
数
とネピア
数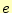 の値を小数点以下20桁表示せよ.
の値を小数点以下20桁表示せよ.
- [練習4]
- 自然対数の関数log(x)の変数xを負の値とした場合,どの ようになるか? プログラムを作って調べよ.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年6月26日