3 複素数と複素関数
3.1 複素関数を使った例
以前のC言語は複素数がサポートされていなかった.数値計算をする場合,複素数が使え ないとかなり不便を強いられる.そのため,複素数が使える FORTRAN から抜け出せない 人が多くいた.新しいC言語では,複素数がサポートされている.これは非常にありがた い.実際に複素数や複素関数を使った例をリスト2に示す.これ は,オイラーが発見した式
| (1) |
の計算結果である.この式はとても不思議で,25年くらい前にはじめてみたときには大変驚いた記憶があ る.それまではなんの関係もないと思っていた円周率
1 #include <stdio.h>
2 #include <complex.h>
3 #include <math.h>
4
5 int main(void){
6 double _Complex z, x;
7
8 x=I*M_PI;
9 z=cexp(x);
10
11 printf("real=%f\timag=%f\n", creal(z),cimag(z));
12
13 return 0;
14 }
real=-1.000000 imag=0.000000このプログラムの各行の内容は,次の通りである.
- 2行目 #include <complex.h>
複素数おほび複素関数を使うために,ヘッダーファイルcomplex.hをインク ルードしている.複素数を使う場合,必ず必要である.
- 6行目 double _Complex z, x;
倍精度複素数型の変数の宣言である.複素数型の変数zとxが使えるよ うになる.
- 8行目 x=I*M_PI;
先に述べたように,M_PIは円周率を表すマクロである.Iは虚数単位 である.したがって,C言語のI*M_PIは,数学の
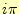 を表す.
を表す.
- 9行目 z=cexp(x);
cexp(x)は,数学の
 を表す.ただし,変数も関数の値も複素数となる.
を表す.ただし,変数も関数の値も複素数となる.
- 11行目 creal(z),cimag(z)
creal(z)で複素数zの実数部を,cimag(z)で虚数部を取り出して いる.
3.2 複素関数の使い方
3.2.1 記述方法
3.2.1.1 ヘッダーファイル
ヘッダーファイルcomplex.hをインクルードする必要がある.プログラムの前の方に,#include <complex.h>
と書く.
3.2.1.2 変数宣言
複素数の計算では,複素数型の変数宣言が必要である.変数宣言の例を,以下に示す.float _Complex a, b, hoge; double _Complex c, d. fuga; long double _Complex e, f, foo;
のようにする.通常は,double _Complexを使うこと.C言語で実数を扱う場合は double,複素数を扱う場合はdouble _Complexとするのが無難である.
3.2.1.3 複素数
虚数単位はIである.数学は小文字を使うが,C言語では大文字である.複素数型の 変数に値を代入するためには,次のようにする.z=x+I*y; w=3.1415+I*2.718281828;
3.2.1.4 四則演算
四則演算は特に気にすることもなく,普通に演算子(+,-,*,/)が使える.
3.2.1.5 複素関数
表3のような関数が用意されている.よほどのことがない限り, 倍精度型を使うこと.| 数学関数名 | 倍精度 | 単精度 | 拡張倍精度 | 戻り値 |
| 三角関数 | csin(x) | csinf(x) | csinl(x) | 複素数 |
| ccos(x) | ccosf(x) | ccosl(x) | 複素数 | |
| ctan(x) | ctanf(x) | ctanl(x) | 複素数 | |
| 逆三角関数 | casin(x) | casinf(x) | casinl(x) | 複素数 |
| cacos(x) | cacosf(x) | cacosl(x) | 複素数 | |
| catan(x) | catanf(x) | catanl(x) | 複素数 | |
| 双曲線関数 | csinh(x) | csinhf(x) | csinhl(x) | 複素数 |
| ccosh(x) | ccoshf(x) | ccoshl(x) | 複素数 | |
| ctanh(x) | ctanhf(x) | ctanhl(x) | 複素数 | |
| 逆双曲線関数 | casinh(x) | casinhf(x) | casinhl(x) | 複素数 |
| cacosh(x) | cacoshf(x) | cacoshl(x) | 複素数 | |
| catanh(x) | catanhf(x) | catanhl(x) | 複素数 | |
| 指数関数 | cexp(x) | cexpf(x) | cexpl(x) | 複素数 |
| 自然対数 | clog(x) | clogf(x) | clogl(x) | 複素数 |
| 絶対値 | cabs(x) | cabsf(x) | cabsl(x) | 実数 |
| 平方根 | csqrt(x) | csqrtf(x) | csqrtl(x) | 複素数 |
| べき乗 | cpow(x,y) | cpowf(x,y) | cpowl(x,y) | 複素数( |
| 実部 | creal(x) | crealf(x) | creall(x) | 実数 |
| 虚部 | cimag(x) | cimagf(x) | cimagl(x) | 実数 |
| 偏角 | carg(x) | cargf(x) | cargl(x) | 実数 |
| 複素共役 | conj(x) | conjf(x) | conjl(x) | 複素数 |
| リーマン球の射影 | cproj(x) | cprojf(x) | cprojl(x) | 複素数 |
3.2.2 コンパイル方法
実数型と同じように,オプション-lmをつける.gcc -o fugafuga hogehoge.c -lm
3.3 練習問題
- [練習5]
- 複素数
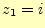 と
と について,以下の値を計算せよ.
について,以下の値を計算せよ.
- 2乗と3乗
- 平方根と立方根
- 絶対値
- 複素共役
- [練習6]
- オイラーの関係式
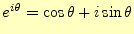 が成
り立つことを,
が成
り立つことを,
 の範囲で調べよ.
この間を360等分して,両辺の値を出力する.
の範囲で調べよ.
この間を360等分して,両辺の値を出力する.
- [練習7]
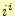 の値を計算してみよ.そして,解析解と比較せよ.
の値を計算してみよ.そして,解析解と比較せよ.
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年6月26日