係数行列
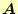 が下三角行列
が下三角行列
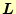 と上三角行列
と上三角行列
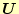 の積に展開でき
たとする.
の積に展開でき
たとする.
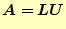 |
(14) |
下三角行列と上三角行列の要素を書き出すと
となる.
このようにLU分解できると,連立1次方程式は
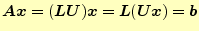 |
(16) |
と書ける.これをさらに書き換えると,
となる.これらの連立方程式の解
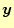 と
と
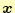 は,それぞれの係数
が三角行列なので容易に計算できる(ガウス消去法と後退代入の説明を見よ).
は,それぞれの係数
が三角行列なので容易に計算できる(ガウス消去法と後退代入の説明を見よ).
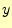 の方は,係数が下三角行列なので
の方は,係数が下三角行列なので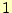 〜
〜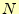 まで前進代入により解ける.
具体的には,
まで前進代入により解ける.
具体的には,
である.この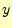 が求まったならば,今度は係数が上三角行列の式(
が求まったならば,今度は係数が上三角行列の式(![[*]](crossref.png) )の
)の
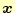 を求める.これは,
を求める.これは,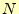 〜
〜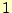 の順序で計算する後
退代入を使う.
の順序で計算する後
退代入を使う.
これらの前進代入と後退代入は,コンピューターにとって非常に簡単に計算できる.これ
は,係数行列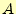 をLU分解できれば,連立方程式は簡単に解けると言っている.次節でLU
分解の方法を詳しく説明する.
をLU分解できれば,連立方程式は簡単に解けると言っている.次節でLU
分解の方法を詳しく説明する.
いったんLU分解が出来てしまえば,式(1)の右辺
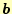 が変わっ
ても,そのLU分解の形を変える必要がない.右辺が変わっても,LU分解は1回で済む.こ
れが,ガウスの消去法と後退代入を組み合わせた方法やガウス・ジョルダン法に比べて,
際立って優れている点である.
が変わっ
ても,そのLU分解の形を変える必要がない.右辺が変わっても,LU分解は1回で済む.こ
れが,ガウスの消去法と後退代入を組み合わせた方法やガウス・ジョルダン法に比べて,
際立って優れている点である.
LU分解するということは,式(15)の
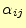 と
と
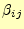 を計算することにほかならない.この式の行列方程式は,
を計算することにほかならない.この式の行列方程式は,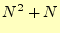 の未知数と
の未知数と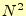 の式を
含む.未知数の数が方程式の数より多いので,
の式を
含む.未知数の数が方程式の数より多いので,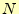 個の未知数を勝手に決めて残りを計算
することが可能である.従って,LU分解は一意に決まらない,計算しやすいように
個の未知数を勝手に決めて残りを計算
することが可能である.従って,LU分解は一意に決まらない,計算しやすいように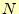 個
の未知数を決めることができる.ここでは,LU分解のクラウト(Crout)のアルゴリズムに
従い,
個
の未知数を決めることができる.ここでは,LU分解のクラウト(Crout)のアルゴリズムに
従い,
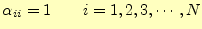 |
(21) |
とする.
それでは,クラウトのアルゴリズムによるLU分解の手順を示すことにする.
-
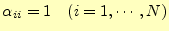 とします.この操作により,解
くべき行列方程式(15)は
とします.この操作により,解
くべき行列方程式(15)は
と変形できる.
- この式を見ると,
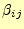 と
と
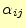 が次に示す順序で簡単に求められ
ることが分かる.まずは式を見て分かるように,
が次に示す順序で簡単に求められ
ることが分かる.まずは式を見て分かるように,
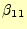 が直ちに計算できる.
次に
が直ちに計算できる.
次に
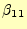 を利用して,
を利用して,
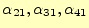 を求める
ことができる.これで,
を求める
ことができる.これで,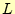 と
と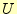 の第1列目が求められた.次に第2列目である.こ
れも
の第1列目が求められた.次に第2列目である.こ
れも
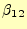 は直ちに計算できる.そうして,これまで分かっている
は直ちに計算できる.そうして,これまで分かっている
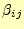 と
と
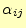 を使うと,
を使うと,
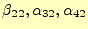 を求めることができる.これで第2列目は終わりで,同じことを繰り返すと,全て
の
を求めることができる.これで第2列目は終わりで,同じことを繰り返すと,全て
の
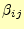 と
と
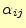 が計算できる.これをアルゴリズムにすると次の
ようになる.
が計算できる.これをアルゴリズムにすると次の
ようになる.
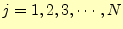 という順序で計算する.
という順序で計算する.
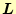 と
と
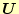 の
の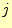 列目を計算することになる.具体的には,以下のようにして,
列目を計算することになる.具体的には,以下のようにして,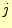 列目の
列目の
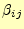 と
と
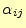 を求める.
を求める.
この方法により,LU分解ができる.次に示すピボット選択をしなければ,アルゴリズムは
非常に単純である.
ここでも,ピボット選択の問題が出てくる.式(24)の
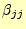 で割る部分である.安定な解を求めるためには,ピボット選択は必要不可欠ということで
ある.完全ピボット選択は複雑なので,部分ピボット選択で十分であろう.
で割る部分である.安定な解を求めるためには,ピボット選択は必要不可欠ということで
ある.完全ピボット選択は複雑なので,部分ピボット選択で十分であろう.
ではどうするかですが,これも途中(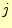 列)まで分解した行列は崩したくない.そのため
には,行列
列)まで分解した行列は崩したくない.そのため
には,行列
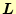 の行を交換し,それに対応した行列
の行を交換し,それに対応した行列
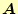 の行を交換すれば問題
がもっとも少なくなる.当然,行列
の行を交換すれば問題
がもっとも少なくなる.当然,行列
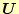 は行も列も変化しない.最終的には行を交換
した行列
は行も列も変化しない.最終的には行を交換
した行列
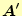 のLU分解が出来る.連立1次方程式を解くときには,同様に
のLU分解が出来る.連立1次方程式を解くときには,同様に
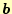 の行も交換しておく.ただし,行の交換であるため,解
の行も交換しておく.ただし,行の交換であるため,解
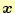 の要素の順序は
入れ替わらない.
の要素の順序は
入れ替わらない.
つぎに,どのようにして交換する行を決めるかである.一般的には,
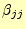 が大き
くなるように選択すれば良い結果が得られる.クラウト法のピボット選択は,次のように
進める.
が大き
くなるように選択すれば良い結果が得られる.クラウト法のピボット選択は,次のように
進める.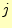 列目のピボットを選択する場合についてである.
列目のピボットを選択する場合についてである.
- まずは,
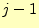 列目までの行列
列目までの行列
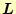 の各行の要素の最大値を1に規
格化する.同時に,対応する行列
の各行の要素の最大値を1に規
格化する.同時に,対応する行列
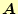 の行も同じ係数を掛ける.
の行も同じ係数を掛ける.
- そうして,
を計算する.これは,式(23)と同じ,
式(24)と
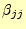 で割ること以外は同じであ
ることに注意が必要である.
で割ること以外は同じであ
ることに注意が必要である.
- 最大の
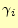 となるものをピボットとして選択する.
となるものをピボットとして選択する.
- 最大のピボットとなる行が分かったので,後は元(規格化前)の
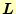 と
と
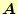 を用いて,式(24)と
を用いて,式(24)と
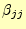 を計算する.
を計算する.
これがピボット探索のルーチンである.実際には,ピボット作成用の関数を作成
して,計算をすることになる.
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年10月25日
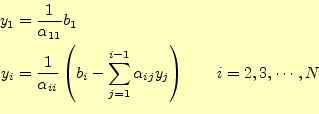
![[*]](crossref.png) )の
)の
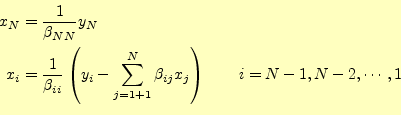
![]() をLU分解できれば,連立方程式は簡単に解けると言っている.次節でLU
分解の方法を詳しく説明する.
をLU分解できれば,連立方程式は簡単に解けると言っている.次節でLU
分解の方法を詳しく説明する.
![]() が変わっ
ても,そのLU分解の形を変える必要がない.右辺が変わっても,LU分解は1回で済む.こ
れが,ガウスの消去法と後退代入を組み合わせた方法やガウス・ジョルダン法に比べて,
際立って優れている点である.
が変わっ
ても,そのLU分解の形を変える必要がない.右辺が変わっても,LU分解は1回で済む.こ
れが,ガウスの消去法と後退代入を組み合わせた方法やガウス・ジョルダン法に比べて,
際立って優れている点である.
![]() 列)まで分解した行列は崩したくない.そのため
には,行列
列)まで分解した行列は崩したくない.そのため
には,行列
![]() の行を交換し,それに対応した行列
の行を交換し,それに対応した行列
![]() の行を交換すれば問題
がもっとも少なくなる.当然,行列
の行を交換すれば問題
がもっとも少なくなる.当然,行列
![]() は行も列も変化しない.最終的には行を交換
した行列
は行も列も変化しない.最終的には行を交換
した行列
![]() のLU分解が出来る.連立1次方程式を解くときには,同様に
のLU分解が出来る.連立1次方程式を解くときには,同様に
![]() の行も交換しておく.ただし,行の交換であるため,解
の行も交換しておく.ただし,行の交換であるため,解
![]() の要素の順序は
入れ替わらない.
の要素の順序は
入れ替わらない.
![]() が大き
くなるように選択すれば良い結果が得られる.クラウト法のピボット選択は,次のように
進める.
が大き
くなるように選択すれば良い結果が得られる.クラウト法のピボット選択は,次のように
進める.![]() 列目のピボットを選択する場合についてである.
列目のピボットを選択する場合についてである.