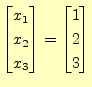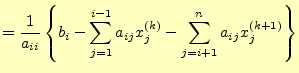2 ガウス・ザイデル法を使った計算

2.1 連立一次方程式

ガウス・ザイデル法のような反復法は大きな連立方程式の計算に適している．しかし，こ こではその計算原理を分かり易くするため，次の連立方程式を計算する．

$$\begin{bmatrix}3 & 2 & 1 \\ 1 & 4 & 1 \\ 2 & 2 & 5 \end{bmatrix} ... ...x}x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix}10 \\ 12 \\ 21 \end{bmatrix}$$ (1)

この方程式の解析解は，

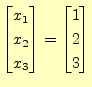$$\begin{bmatrix}x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix}1 \\ 2 \\ 3 \end{bmatrix}$$ (2)

であるが，ガウス・ザイデル法でこれを求めることにする．前に示したようにガウス・ ザイデル法の漸化式は

$$x_i^{(k+1)} =a_{ii}^{-1}\left\{b_i-\left[ a_{i1}x_1^{(k+1)}+a_{i2}x_2^{(k+1)}... ...i-1}x_{i-1}^{(k)}+a_{ii+1}x_{i+1}^{(k)}\cdots +a_{in}x_{n}^{(k)}\right]\right\}$$

$$=\frac{1}{a_{ii}}\left\{b_i -\sum_{j=1}^{i-1}a_{ij}x_j^{(k)} -\sum_{j=i+1}^{n}a_{ij}x_j^{(k+1)} \right\}$$ (3)

である．これは，反復の$k$番目の近似解から，より精度の良い$k+1$番目の解を求める方法を表し ている．

これを，式(1)に当てはめると

$$x_1^{(k+1)}=\frac{1}{3}\left[10-2x_2^{(k)}-x_3^{(k)}\right]$$ (4)

$$x_2^{(k+1)}=\frac{1}{4}\left[12-x_1^{(k+1)}-x_3^{(k)}\right]$$ (5)

$$x_3^{(k+1)}=\frac{1}{5}\left[21-2x_1^{(k+1)}-2x_2^{(k+1)}\right]$$ (6)

である．当然，これは $x_1^{(k+1)}\rightarrow x_2^{(k+1)}\rightarrow x_3^{(k+1)}$の順序で計算を進める．もう少しくだけた見方をする と，この式は連立方程式式(1)

$$3x_1+2x_2+x_3=10$$ (7)

$$x_1+4x_2+x_3=12$$ (8)

$$2x_1+2x_2+5x_3=21$$ (9)

から，各行の $x_1, x_2, x_3$を解いている式と

$$x_1=\frac{1}{3}\left(10-2x_2-x_3\right)$$ (10)

$$x_2=\frac{1}{4}\left(12-x_1-x_3\right)$$ (11)

$$x_3=\frac{1}{5}\left(21-2x_1-2x_2\right)$$ (12)

と同一である．式(7)から式(10)を，式(8) から式(11)を，式(9)から式(12)を導いてい るのである．ガウス・ザイデル法の漸化式(4),(5),(6)は， 連立方程式を変形した式(10),(11),(12)とそっ くりである．最初にガウス・ザイデル法を考えた人(ザイデル???)は，連立方程 式を式(10)〜(12)のように変形して，繰り返し計算を行えば 真の解に近づくと考えたのだろう．ちょっと数値計算になれた者であればすぐに気がつくア ルゴリズムである．

2.2 プログラム例

漸化式が求められたので，実際のプログラムを書いてみよう．プログラムの例をリスト 1に示しておくので，よく理解せよ．

   1 #include <stdio.h>
   2 #include <math.h>
   3 #define N (3)               // 連立方程式の大きさ
   4 #define EPS (1e-15)         // 計算誤差の許容値
   5 
   6 int main(void){
   7   double a[N+1][N+1], x[N+1], b[N+1];
   8   double dx, absx, sum, new;
   9   int i,j;
  10 
  11   a[1][1]=3.0;  a[1][2]=2.0;  a[1][3]=1.0;  // 係数行列
  12   a[2][1]=1.0;  a[2][2]=4.0;  a[2][3]=1.0;
  13   a[3][1]=2.0;  a[3][2]=2.0;  a[3][3]=5.0;
  14 
  15   b[1]=10.0;                         // 同次項
  16   b[2]=12.0;
  17   b[3]=21.0;
  18 
  19   x[1]=0.0;                          // 近似解の初期値
  20   x[2]=0.0;
  21   x[3]=0.0;
  22 
  23   do{                                // 反復計算のループ
  24     dx=0.0;
  25     absx=0.0;
  26 
  27     for(i=1;i<=N;i++){
  28       sum=0;
  29       for(j=1;j<=N;j++){
  30 	if(i != j){
  31 	  sum+=a[i][j]*x[j];
  32 	}
  33       }
  34 
  35       new=1.0/a[i][i]*(b[i]-sum);   // 反復計算後の近似解
  36       dx+=fabs(new-x[i]);           // 近似解の変化量を加算
  37       absx+=fabs(new);              // 近似解の総和計算
  38       x[i]=new;                     // 新しい近似解を代入
  39     }
  40    
  41   }while(dx/absx > EPS);            // 計算終了条件
  42  
  43   for(i=1;i<=N;i++){
  44     printf("x[%d]=%25.20f\n",i,x[i]);
  45   }
  46 
  47   return 0;
  48 }

ホームページ: Yamamoto's laboratory
著者: 山本昌志