2 円周率の計算

円周率10万桁まで精度良く計算するプログラムを作成する．これは，必須ではないが，興 味のある者はプログラムを作成せよ．この部分は，山形大学の新関久一さんの「プログラ ミング演習 III」を参考にさせてもらっている．最初に，ヒントとして，長桁計算のプロ グラムを示す．

2.1 長桁計算

円周率を10万桁まで求めようとすると，長桁の計算が必要になる．しかし，C言語の倍精 度実数は20桁程度しか有効数字がない．そこで，長桁計算を考えることにする．人間は時 間と紙さえあれば，いくらでも長い桁の計算ができる．ただの計算なので，人間ができて コンピューターができないわけがない．人間と同じことをコンピューターにやらせれば良 いのである．人間と同じように，コンピューターに長桁の筆算の計算をさせる．紙の代わ りにデータは配列に記憶させるだけである．

これを最初から考えるのは，初心者には少し難しい．そこで，参考のために，リスト 1にプログラムを載せておく．このプログラムでは，非常に大きな桁 数の2つの整数を入力して，その和と差を計算することができる．

このプログラムでは，負の値は10の補数を用いている．もしある数が負の整数であれば， その絶対値の各桁を9から差し引いて，最後に1を加えている．この辺のところは，3年生 の電子計算機の授業で教えたはずである²． ただ，そのときは2進法を使っていたので，2の補数だったが，考え方は同じである．

   1 #include <stdio.h>
   2 #include <string.h>
   3 #include <stdlib.h>
   4 #define N 32768
   5 #define RADIX 10
   6 
   7 void lf_scan(int n[]);
   8 void lf_plus();
   9 void lf_minus();
  10 void lf_print(int n[]);
  11 void lf_complement(int n[]);
  12 void prt_bit(int n[]);
  13 int a[N], b[N], Acc[N];
  14 
  15 /*================================================================*/
  16 /*   main                                                         */
  17 /*================================================================*/
  18 int main(void){
  19 
  20   lf_scan(a);
  21   lf_scan(b);
  22   lf_plus();
  23   lf_print(Acc);
  24   lf_minus();
  25   lf_print(Acc);
  26 
  27   return 0;
  28 }
  29 
  30 
  31 /*================================================================*/
  32 /*   lf_scan                                                      */
  33 /*================================================================*/
  34 void lf_scan(int n[]){
  35   unsigned char key_in[N];
  36   int i,l,flag=0;
  37 
  38   scanf("%s",key_in);
  39 
  40   l=strlen(key_in);
  41 
  42   if(key_in[0] == '-'){
  43     flag=1;
  44     for(i=1; i<l; i++){
  45       key_in[i-1]=key_in[i];
  46     }
  47     l--;
  48   }
  49 
  50   for(i=0;i<l;i++){
  51     n[i]=(unsigned int)key_in[l-1-i]-48;
  52   }
  53 
  54   if(flag==1)lf_complement(n);
  55 }
  56   
  57 /*================================================================*/
  58 /*   lf_plus                                                      */
  59 /*================================================================*/
  60 void lf_plus(){
  61   int i;
  62 
  63   for(i=0;i<N;i++) Acc[i] = a[i]+b[i];    
  64 
  65   for(i=0; i<N-1; i++){
  66     if(Acc[i] > 9)Acc[i+1]++;
  67     Acc[i]%=RADIX;
  68   }
  69 
  70   Acc[N-1]%=RADIX;
  71 
  72 }
  73 
  74 /*================================================================*/
  75 /*   lf_minus                                                     */
  76 /*================================================================*/
  77 void lf_minus(){
  78 
  79   lf_complement(b);
  80   lf_plus();
  81   
  82 }
  83 
  84 /*================================================================*/
  85 /*   lf_print                                                     */
  86 /*================================================================*/
  87 void lf_print(int n[]){
  88   int i,j,flag=0;
  89 
  90   i=N-1;
  91 
  92   if(n[i]>4){
  93     flag=1;
  94     lf_complement(n);
  95     printf("-");
  96   }
  97 
  98   while(n[i]==0 && i>0) i--;
  99   for(j=i;j>=0;j--)printf("%d",n[j]);
 100   
 101   if(flag==1)lf_complement(n);
 102 
 103   printf("\n");
 104 
 105 
 106 }
 107 
 108 /*================================================================*/
 109 /*   complement                                                   */
 110 /*================================================================*/
 111 void lf_complement(int n[]){
 112   int i;
 113 
 114   for(i=0; i<N; i++) n[i]=9-n[i];
 115 
 116   n[0]++;
 117 
 118   i=0;
 119   while(n[i]==10 && i < N){
 120     n[i]=0;
 121     n[i+1]++;
 122     i++;
 123   }
 124 }

2.2 円周率の計算

2.2.1 円周率の計算方法

足し算と引き算の長桁の計算方法は分かった．わり算も同じである．後は自分で考えて， マチンの公式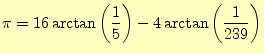

$$\pi=16\arctan\left(\frac{1}{5}\right)-4\arctan\left(\frac{1}{239}\right)$$

とテイラー展開

$$\arctan(x) =x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\frac{x^9}{9}-\frac{x^{11}}{11}+\frac{x^{13}}{13}-\frac{x^{15}}{15}+\cdots$$

$$=\sum_{n=1}^\infty(-1)^{n-1}\frac{x^{2n-1}}{2n-1}$$

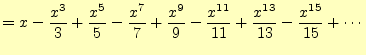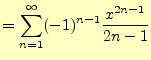を用いて，10万桁を計算するプログラムを作成せよ．

2.2.2 10万桁の値

計算結果はわかりやすいように，以下のように10万桁の値を表示させよ．これから分かる ように，10万桁の円周率は， $\pi=3.1415926535897932\cdots 080565549362 4646$となる． この表最後の値の6が10万桁目である．自分のプログラムの結果が正しいか否かの判定に この表を使うと良い．

3.1415 9265 3589 7932 3846 2643 3832 7950 2884 1971 6939 9375
  1058 2097 4944 5923 0781 6406 2862 0899 8628 0348 2534 2117
  0679 8214 8086 5132 8230 6647 0938 4460 9550 5822 3172 5359
  4081 2848 1117 4502 8410 2701 9385 2110 5559 6446 2294 8954
  9303 8196 4428 8109 7566 5933 4461 2847 5648 2337 8678 3165
  2712 0190 9145 6485 6692 3460 3486 1045 4326 6482 1339 3607
  2602 4914 1273 7245 8700 6606 3155 8817 4881 5209 2096 2829
  2540 9171 5364 3678 9259 0360 0113 3053 0548 8204 6652 1384
  1469 5194 1511 6094 3305 7270 3657 5959 1953 0921 8611 7381
  9326 1179 3105 1185 4807 4462 3799 6274 9567 3518 8575 2724
  8912 2793 8183 0119 4912 9833 6733 6244 0656 6430 8602 1394
  9463 9522 4737 1907 0217 9860 9437 0277 0539 2171 7629 3176
  7523 8467 4818 4676 6940 5132 0005 6812 7145 2635 6082 7785


　このあたりは長いので省略


  0491 5378 8541 3909 4245 3169 1719 9876 2894 1277 2211 2946
  4568 2948 6028 1493 1815 6024 9677 8879 4981 3777 2162 2935
  9437 8110 0444 8060 7976 7242 9276 2495 1078 4153 4464 2915
  0842 7645 2000 2042 7694 7069 8041 7758 3220 9097 0202 9165
  7347 2515 8290 4630 9103 5903 7842 9775 7265 1720 8772 4474
  0952 2671 6630 6005 4697 1638 7943 1711 9687 3484 6887 3818
  6656 7512 7929 8575 0163 6341 1314 6275 3049 9019 1356 4682
  3804 3299 7069 5770 1507 8933 7728 6580 3571 2790 9137 6742
  0805 6554 9362 4646

2.2.3 スピードアップ

プログラムを工夫して，計算のスピードアップに挑戦せよ．

2.3 課題提出要領

提出方法は，次の通りとする．

期限	前期中ならいつでも
用紙	A4
提出場所	山本まで直接，手渡し．
表紙	表紙を1枚つけて，以下の項目を分かりやすく記述すること．
	授業科目名「計算機応用」
	課題名「課題　長桁の円周率の計算」
	5E    学籍番号    氏名
	提出日
内容	計算アルゴリズムを分かりやすく記述すること．
	計算に工夫した点
	ソースリスト

ホームページ: Yamamoto's laboratory
著者: 山本昌志