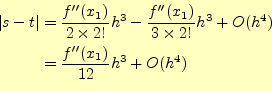定積分,
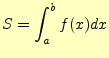 |
(3) |
の近似値を数値計算で求めることを考える.積分の計算は,先に示したように面積の計算
であるから,図2のように台形の面積の和で近似ができるであ
ろう.積分の範囲![$ [a,b]$](img6.png) を
を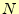 等分した台形で近似した面積Tは,
等分した台形で近似した面積Tは,
となる.これが数値積分の台形公式である.なんのことはない,積分を台形の面積に置き
換えているだけである.
台形公式による数値積分では,分割数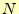 を大きくするとその誤差は小さくなることは直
感で分かる.それでは,分割数を増やしていくとどのように精度が良くなるのか考えてみ
よう.
を大きくするとその誤差は小さくなることは直
感で分かる.それでは,分割数を増やしていくとどのように精度が良くなるのか考えてみ
よう.
まずは,式(4)のある一つの台形の面積と実際の積分の値を比較する.台
形の面積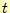 は,台形公式より,
は,台形公式より,
となる.これを実際の積分
と比較することにする.これら2つの式の形がぜんぜん違うので比較できないと考えるだろ
う.このような場合の常套手段がある.ちょっとした違いについて論じる時には,テーラー
展開を使う.式(5)を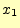 の周りで,テイラー展開すると
の周りで,テイラー展開すると
となる.これが台形の面積のテイラー展開である.一方,積分の
式(6)もテイラー展開する.これは,
となる.この2つの式(7)と
( 8)が台形での近似と
まっとうに積分を行ったときのテイラー展
開を表す.これらの式を比べると,刻み巾 の2 次まで一致している.これは,直感的
には次のように考えることができる.
の2 次まで一致している.これは,直感的
には次のように考えることができる.
- 台形公式では
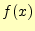 を直線で近似しているので,被積分関数は
を直線で近似しているので,被積分関数は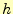 の1次の精度がある.
の1次の精度がある.
- 台形の一つの面積は,被積分関数に
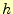 を乗じることにより得られる.したがって,
面積は
を乗じることにより得られる.したがって,
面積は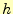 の2次の精度になる.
の2次の精度になる.
これまでの結果から,台形式の積分の誤差は の3次よりも高次が問題となり,
の3次よりも高次が問題となり,
と表せる.即ち,積分を台形で近似したひとつの区間の誤差は,刻み幅の で効いて
くるのである.従って,積分のトータルの誤差は,それを区間の個数
で効いて
くるのである.従って,積分のトータルの誤差は,それを区間の個数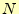 を乗じた
を乗じた
となる.積分の誤差は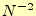 に比例する.分割数を10倍にすれば,積分の誤差は1/100になるわけである.
に比例する.分割数を10倍にすれば,積分の誤差は1/100になるわけである.
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年12月20日
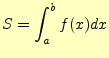
![]() は,台形公式より,
は,台形公式より,