Subsections
ラグランジュの補間はデータ点数が増えてくると関数が振動し,補間の精度が悪くなるの
は先に述べたとおりである.そこで,補間する領域をデータ間隔
![$ [x_i,x_{i+1}]$](img44.png) に区切
り,その近傍の値を使い低次の多項式で近似することを考える.区分的に近似関数を使う
ことになるが,上手に近似をしないと境界でその導関数が不連続になる.導関数が連続にな
るように,上手に近似する方法がスプライン補間(spline interpolation)である.
に区切
り,その近傍の値を使い低次の多項式で近似することを考える.区分的に近似関数を使う
ことになるが,上手に近似をしないと境界でその導関数が不連続になる.導関数が連続にな
るように,上手に近似する方法がスプライン補間(spline interpolation)である.
ここでは,通常よくつかわれる3次のスプライン補間について説明する.3次関数を補間に
使うため,そう呼ばれている.これ以降の説明は,文献[1]を参考にした.
データは先と同じように
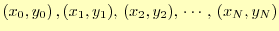 と
する.そして,区間
と
する.そして,区間
![$ [x_j,x_{j+1}]$](img46.png) で補間に使う関数を
で補間に使う関数を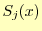 とする.この様子を図
5に示す.
とする.この様子を図
5に示す.
3次のスプライン補間を考えるので,区分多項式は
となる.この
 を求めることが,スプライン補間の中心的な問題
となる.
を求めることが,スプライン補間の中心的な問題
となる.
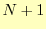 個のデータ数があるため,区分多項式は
個のデータ数があるため,区分多項式は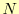 個ある.したがって,区分多項式の係数
である未知数は
個ある.したがって,区分多項式の係数
である未知数は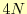 個あることになる.これを求めるためには,
個あることになる.これを求めるためには, 個の方程式が必要
となる.3次のスプライン補間に以下の条件を課して,その係数を求めることにする.
個の方程式が必要
となる.3次のスプライン補間に以下の条件を課して,その係数を求めることにする.
- [条件1]
- 全てのデータ点を通る.各々の
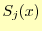 に対して両端での値が決まる
ため,
に対して両端での値が決まる
ため, 個の方程式ができる.
個の方程式ができる.
- [条件2]
- 各々の区分補間式は,境界点の1次導関数は連続とする.これにより,
 個の方程式ができる
個の方程式ができる
- [条件3]
- 各々の区分補間式は,境界点の2次導関数も連続とする.これにより,
 個の方程式ができる.
個の方程式ができる.
以上の3つの条件を課すと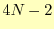 個の方程式で未知数である係数の関係を表現できる.実
際,未知数は
個の方程式で未知数である係数の関係を表現できる.実
際,未知数は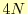 個なので,2個方程式が不足している.この不足を補うために,いろい
ろな条件が考えられるが,通常は両端
個なので,2個方程式が不足している.この不足を補うために,いろい
ろな条件が考えられるが,通常は両端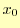 と
と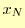 での2次導関数の値を0とする.すなわ
ち,
での2次導関数の値を0とする.すなわ
ち,
 である.このようにす
ることにより,全体の関数の形にもっとも影響を少なくすることができる.これを自然
スプライン(natural spline)という.自然スプライン以外には,両端の1次導関数の値を
指定するものもある.
である.このようにす
ることにより,全体の関数の形にもっとも影響を少なくすることができる.これを自然
スプライン(natural spline)という.自然スプライン以外には,両端の1次導関数の値を
指定するものもある.
これで全ての条件が決まった.あとは,この条件に満たす連立方程式を求めるだけである.
このように,必要な条件が決まった場合, 個の未知数
個の未知数
 を既知の
を既知の
 を使って連立方程式を作るのが普通である.これも可能であるが,少し手間
を省くために,
を使って連立方程式を作るのが普通である.これも可能であるが,少し手間
を省くために,
- これら
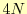 個の未知数を
個の未知数を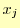 と
と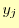 ,さらに
,さらに における2次導関数の値を
における2次導関数の値を
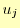 で表現する.
で表現する.
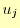 が満たす連立方程式を作り,
が満たす連立方程式を作り, を解く.
を解く.
- 既知の
 と
と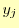 と連立方程式により求められた
と連立方程式により求められた を用いて,区分多項式の
係数
を用いて,区分多項式の
係数
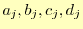 を計算する.
を計算する.
というアプローチで問題を解く.ここで,本当に未知数
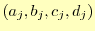 を
を
 で表現することができるのか--という疑問が湧く者もいるだろう.これは,先の連
立方程式を作る条件を上手に使うことにより可能なのである.また,このような方法は,
問題解決の遠回りをしているように思えるが,以降の説明を見ると実際にはかなり簡潔に
なることがわかるので我慢して読んで欲しい.
で表現することができるのか--という疑問が湧く者もいるだろう.これは,先の連
立方程式を作る条件を上手に使うことにより可能なのである.また,このような方法は,
問題解決の遠回りをしているように思えるが,以降の説明を見ると実際にはかなり簡潔に
なることがわかるので我慢して読んで欲しい.
これは,
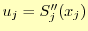 から求めることができ
る.式(5)から,
から求めることができ
る.式(5)から,
 |
(7) |
となる. の時,これは
の時,これは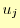 となるので,
となるので,
が直ちに導かれる.これで,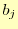 を
を で表現できたことになる.
で表現できたことになる.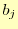 を表現するた
めには,
を表現するた
めには,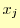 と
と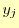 を使っても良かったが,ここではたまたま必要なかったのである.
を使っても良かったが,ここではたまたま必要なかったのである.
これは,2次導関数が区分多項式の境界で等しいという条件から
導くことができる.先ほどは区分多項式の左端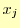 を考えた.次に右端
を考えた.次に右端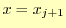 を考
えることにする.右端の導関数は,
を考
えることにする.右端の導関数は,
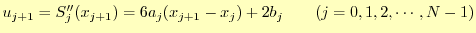 |
(9) |
となる.これから,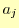 は
は
と導くことができる.これで,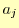 を
を と
と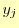 と
と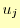 で表現できたことになる.
で表現できたことになる.
これは,区分多項式は全てのデータ点上を通過するという条件
から導くことができる.まずは,多項式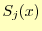 の左端
の左端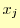 を考える.ここでは,
を考える.ここでは,
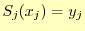 なので,式(5)に代入すると
なので,式(5)に代入すると
が直ちに導ける.これで,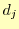 を
を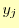 で表現できたことになる.
で表現できたことになる.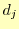 の表現には,
の表現には,
 と
と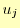 はたまたま不要であった.
はたまたま不要であった.
これもまた,区分多項式は全てのデータ点上を通過するという条件
から導くことができる.今度は,多項式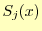 の右端
の右端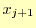 である.ここでは,
である.ここでは,
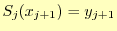 なので,式(5)に代入すると
なので,式(5)に代入すると
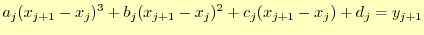 |
(12) |
が導ける.式
(8),(10),(11)を用いる
と,
となる.これで, を
を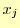 と
と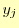 と
と で表現できたことになる.
で表現できたことになる.
以上で,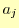 と
と ,
,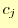 ,
, が
が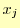 と
と ,
, で表せたことになる.
で表せたことになる.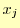 と
と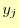 はデータ点なので,既知である.したがって,
はデータ点なので,既知である.したがって,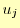 が分かれば,補間に必要な係
数が全て分かるのである.また,連立方程式の[条件1]と[条件3]も満
たしている.従って,[条件2]を満たすように
が分かれば,補間に必要な係
数が全て分かるのである.また,連立方程式の[条件1]と[条件3]も満
たしている.従って,[条件2]を満たすように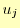 を決めれば良いことになる.
すると全ての区分多項式の係数が分かるのである.
を決めれば良いことになる.
すると全ての区分多項式の係数が分かるのである.
先に述べたように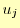 は,1次導関数が境界点で等しいという条件から決める.次の式を
使うのである.
は,1次導関数が境界点で等しいという条件から決める.次の式を
使うのである.
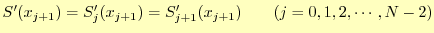 |
(14) |
これと式(5)から,
 |
(15) |
となる.あとは,この式の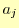 と
と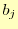 ,
,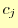 を
を と
と ,
, で
表して,
で
表して,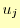 の連立方程式にするだけである.最終的に式は,
の連立方程式にするだけである.最終的に式は,
となる.この方程式は,
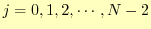 で成り立つ.したがって,式の数は,
で成り立つ.したがって,式の数は,
 個である.
個である.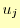 の数は
の数は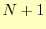 個であるが,
個であるが, としたので,未知の
としたので,未知の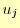 は
は
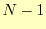 個である.式(16)を解くことにより,全ての
個である.式(16)を解くことにより,全ての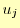 が
決定できる.これが決まれば,
が
決定できる.これが決まれば,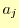 と
と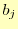 ,そして
,そして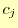 が計算できる.
が計算できる.
 を代入した連立1次方程式は,
を代入した連立1次方程式は,
となる.ただし,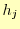 と
と は以下のとおり.
は以下のとおり.
いうまでもないと思うが,スプライン補間を行う区分多項式(5)は,
以下の手順で求める.
- 連立方程式(17)を計算して,各点での二次の導関数の値
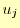 を求める.
を求める.
- 区分多項式の係数
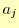 と
と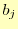 ,
,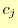 ,
,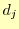 を式(10),
(8),(13),(11)を
計算する.
を式(10),
(8),(13),(11)を
計算する.
区分多項式が分かれば,補間の値計算できる.
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
2008-11-23
![]() と
する.そして,区間
と
する.そして,区間
![]() で補間に使う関数を
で補間に使う関数を![]() とする.この様子を図
5に示す.
とする.この様子を図
5に示す.
![]() 個のデータ数があるため,区分多項式は
個のデータ数があるため,区分多項式は![]() 個ある.したがって,区分多項式の係数
である未知数は
個ある.したがって,区分多項式の係数
である未知数は![]() 個あることになる.これを求めるためには,
個あることになる.これを求めるためには,![]() 個の方程式が必要
となる.3次のスプライン補間に以下の条件を課して,その係数を求めることにする.
個の方程式が必要
となる.3次のスプライン補間に以下の条件を課して,その係数を求めることにする.
![]() 個の方程式で未知数である係数の関係を表現できる.実
際,未知数は
個の方程式で未知数である係数の関係を表現できる.実
際,未知数は![]() 個なので,2個方程式が不足している.この不足を補うために,いろい
ろな条件が考えられるが,通常は両端
個なので,2個方程式が不足している.この不足を補うために,いろい
ろな条件が考えられるが,通常は両端![]() と
と![]() での2次導関数の値を0とする.すなわ
ち,
での2次導関数の値を0とする.すなわ
ち,
![]() である.このようにす
ることにより,全体の関数の形にもっとも影響を少なくすることができる.これを自然
スプライン(natural spline)という.自然スプライン以外には,両端の1次導関数の値を
指定するものもある.
である.このようにす
ることにより,全体の関数の形にもっとも影響を少なくすることができる.これを自然
スプライン(natural spline)という.自然スプライン以外には,両端の1次導関数の値を
指定するものもある.
![]() 個の未知数
個の未知数
![]() を既知の
を既知の
![]() を使って連立方程式を作るのが普通である.これも可能であるが,少し手間
を省くために,
を使って連立方程式を作るのが普通である.これも可能であるが,少し手間
を省くために,
![]() と
と![]() ,
,![]() ,
,![]() が
が![]() と
と![]() ,
,![]() で表せたことになる.
で表せたことになる.![]() と
と![]() はデータ点なので,既知である.したがって,
はデータ点なので,既知である.したがって,![]() が分かれば,補間に必要な係
数が全て分かるのである.また,連立方程式の[条件1]と[条件3]も満
たしている.従って,[条件2]を満たすように
が分かれば,補間に必要な係
数が全て分かるのである.また,連立方程式の[条件1]と[条件3]も満
たしている.従って,[条件2]を満たすように![]() を決めれば良いことになる.
すると全ての区分多項式の係数が分かるのである.
を決めれば良いことになる.
すると全ての区分多項式の係数が分かるのである.
![]() を代入した連立1次方程式は,
を代入した連立1次方程式は,
![$\displaystyle =6\left[\frac{y_{j+1}-y_j}{h_j} -\frac{y_j-y_{j-1}}{h_{j-1}}\right]$](img166.png)