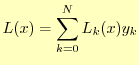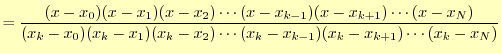Subsections
ある物理量を測定して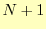 個の値が得られたとする.それらは,
個の値が得られたとする.それらは,
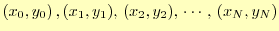 の2次元座標で表すことが
できる.この全ての点を通る関数を求めることが補間法の課題である.N次関数を使えば
その目的が達成できると容易に分かる.データが2個であれば1次関数,3個であれば2次関
数というようにである.一般的に
の2次元座標で表すことが
できる.この全ての点を通る関数を求めることが補間法の課題である.N次関数を使えば
その目的が達成できると容易に分かる.データが2個であれば1次関数,3個であれば2次関
数というようにである.一般的に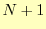 個のデータの場合,
個のデータの場合,
と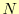 次関数を用いて補間するわけである.この係数
次関数を用いて補間するわけである.この係数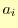 を求めれば,補間の関数が求められたこ
とになる.この係数は,N+1元の連立1次方程式を解くことにより求めることができる.
を求めれば,補間の関数が求められたこ
とになる.この係数は,N+1元の連立1次方程式を解くことにより求めることができる.
この連立方程式の計算にはかなりの時間が必要であるが,それに代わるもっと良い方法が
ある.ここでは,N次関数で表現できれば良いわけで,次のようにする.
この式(2)を見ると,
- 各項の分母は定数で,分子は
 次関数となっている.全て
の項はN次関数になっているので,この式は
次関数となっている.全て
の項はN次関数になっているので,この式は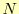 次関数(
次関数(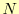 次多項式)である.
次多項式)である.
 に
に
 を代入すると,
を代入すると, の値は
の値は
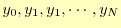 になる.したがって,この
になる.したがって,この 次関数は全てのデータ点
次関数は全てのデータ点
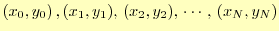 を
通過している.
を
通過している.
となっている.これは,表現こそ違うものの式(1)と同じである.式(1)の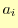 を連立方程式を解くことにより補間の関数を求める必要は無く,式
(2)を使えばよいということである.この補
間をラグランジュの補間多項式(Lagrange's interpolating polynomial)という.式
(2)をもうちょっと格好良く書けば,
を連立方程式を解くことにより補間の関数を求める必要は無く,式
(2)を使えばよいということである.この補
間をラグランジュの補間多項式(Lagrange's interpolating polynomial)という.式
(2)をもうちょっと格好良く書けば,
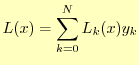 |
(3) |
ただし,
となる. は和の記号であるが,ここで使っている
は和の記号であるが,ここで使っている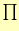 は積の記号である.
補間の点数が増えてくると,ラグランジュの補間の近似の精度が悪くなることがある.そ
の具体例を図4に示す.これから,補間の関数
が振動し,端の方ではかなり精度が悪いことがわかる.ラグランジュの補間では,補間の点数が増えてくると大きな振動が発
生して,もはや補間とは言えなくなることがある.ラグランジュの補間には常にこの危険
性が付きまとうので,データ点数が多い場合は良い方法ではない.ほかの補間を選択しな
くてはならない.
は積の記号である.
補間の点数が増えてくると,ラグランジュの補間の近似の精度が悪くなることがある.そ
の具体例を図4に示す.これから,補間の関数
が振動し,端の方ではかなり精度が悪いことがわかる.ラグランジュの補間では,補間の点数が増えてくると大きな振動が発
生して,もはや補間とは言えなくなることがある.ラグランジュの補間には常にこの危険
性が付きまとうので,データ点数が多い場合は良い方法ではない.ほかの補間を選択しな
くてはならない.
図 4:
ラグランジュ補間の問題点.
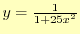 を10点で補間
(点線)したが,両端で振動する.
を10点で補間
(点線)したが,両端で振動する.
|
|
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
2008-11-23