2 エルステッドの発見とアンペールの法則
2.1 磁石
磁石が鉄などの磁性体を引きつけることはよく知られている.諸君は,これまで学習して きた静電的な作用よりも,磁石による作用の方がおなじみかもしれない.磁石のN極とN極, あるいはS極とS極は反発し,N極とS極は引きつけあう.これは,静電場の時に学習したクー ロンの法則の電荷の作用と似ている.磁荷の間に働く力を記述した磁荷におけるクーロン の法則と言うものがある.それは,N極の磁荷を正の値,S極の磁荷を負の値で表し 2,それらの間に働く力の大きさがとなることを示す.ここで,
このように電荷と磁荷はよく似ているが,決定的に異なることがある.電荷は単独で取り 出すことができるが,磁荷は絶対に単独では存在しないのである4.このことは,図1で示すように,磁石を 半分にしてやはりN極とS極があり,それを半分にしてもその断片にも両方の極が存在する ことからも分かる.N極あるいはS極のみの断片は作れないのである.それに対して,電荷 の場合,図2のように帯電した棒を分割すると,正または負のみに帯電し た断片を作ることができるのである.
電荷の場合と異なり単独の磁荷が存在しないと言うことは,式(1) が成り立つ状況は自然には起きえないと言うことである.しかし,磁荷の考えが全く間違っ ているとも言えない場合がある.適当に,正負の磁荷が等量分布していると仮定すると, 観測される磁場と同じものを計算上,作ることが可能である.これは計算のテクニック 上で正しい磁場を作っているにすぎず,単独の磁荷はやはり存在しないことを忘れてはな らない.このテクニックは磁石の磁場を考える場合使われることがある.
電荷のクーロンの法則を使うことは多いが,磁荷の式(1)はほとん ど使われない.少なくとも,私は一回も使ったことがない.したがって,諸君は磁荷のクー ロンの法則は忘れて良い.
それならば,クーロンはこの磁荷の式(1)をどのようにして発見し たのであろうか?.興味があるものは,実験方法について,調べよ.
2.2 電流の磁気作用
2.2.1 電流が磁石に作用することの発見
最初に磁石による力,磁力を発見したのは誰かは分からないが,その解析的な研究の先鞭 をつけたのは,コペンハーゲン大学のエルステッド教授(Hans Christian Oersted, 1777-1851)であろう.彼は,1819年から1820年の冬に,電気学や磁気学の講義をしていた. 当時,電流と電荷の間には何か関係があると考えていた人がいた.どちらも,触るとビリッ とするからである.なんとも,頼りない理由ではあるが,そう考えたのは偉い.ただ,エ ルステットの方は,少し変わっていて,電流と磁石になんらか関係があると考えたようで ある.どのようにして,この考えに至ったかは分からないが,電流を流すと方位磁石は力を受け て,方向が変わると考えた.磁石は力を受けて,電流と同じ方向,あるいは反対の方向に 向くと考えた.これはもっともなことで,電線に流れている電流が,磁石の北の先端が受 ける力は,対称性から考えて,右や左であるわけがない.電流と同じ方向か,その反対で ある.そこで,学生の前で,図3のように,磁石と電線を配置して, スイッチを入れた.結果は,期待に反して,磁石は動かなかったのである.これは,磁石 の方向と電流が作る磁場の方向が一致していたために動かなかったのである.ここで,電 流を反対にすれば,磁石が180度回転して,それはドラマチックなことが起きたはずであ るが,なぜかエルステットは,反対に電流を流していない.それにしても,1/2の確率で エルステットは運がなかった.
しばらく,自分の考えがうまくいかないことに,悶々としていたエルステットは,何を思っ たか,あるいは実験を間違えたか,磁石と電線を同じ方向に向けて,電流を流した.そう すると,磁石が90度回ったのである.これには,エルステットも驚いたに違いない.対称 性から考えて,どうしてもありえないことが起こったのである5.1820年の春のことである.エルステットはなかなか納 得がいかなかったが,実験を繰り返し,その事実を認めた.そして,その発見について, その年の7月に報告書を書いた.
この報告書が他の研究所に届くや否や,多くの実験が行われ,新たな発見が相次いだ.
2.2.2 磁場
エルステッドの実験結果が各地に伝わると,ビオ(Biot)とサバール(Savart),そしてアン ペール(Ampere)がより精密で完全な実験を行った.そして,2本の平行な導線間には力が 働くことがわかった.長さである6.ここで,
この電流が流れる導体間に働く力について,近接作用の考えを取り入れることにしよう.
電流は場を作り,その場からもう一方の導線に力が作用すると考える.この場を磁場![]() と言
い,それを用いると,式(2)は,
と言
い,それを用いると,式(2)は,
| (3) | ||
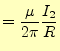 |
(4) |
となる.磁場
この磁場については,導線の方向を変えたりして詳細に調べられて.その結果,1本の直 線電流が作る磁場は,
となることが分かった.これがビオとサバールが最初に実験によって発見した結果である. 有名なジャクソンの電磁気学 [1]には,これをビオ-サバール の法則と書いている.普通,ビオ-サバールの法則は後から出てくる式()を指す.
本講義では,実験的に求められた式(5)を出発点と して,静磁場の理論を構築する.静電場の場合,クーロンの法則を出発点として全 ての式を導いた.それと同様のことを静電場で行う.静電場との対応を考えると,後で出 てくるビオ-サバールの法則の式(12)から議論をはじめると計算が簡単で良い.しか し,式(12)を直感的に理解することは不可能である.なにせ,電流が途中で切れてい る.電荷保存則が成り立っていない--そんなこと想像できるか!!
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年7月25日
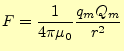
![\includegraphics[keepaspectratio, scale=0.7]{figure/magnet.eps}](img5.png)
![\includegraphics[keepaspectratio, scale=0.7]{figure/charge.eps}](img6.png)
![\includegraphics[keepaspectratio, scale=0.7]{figure/mag_not_move.eps}](img7.png)
![\includegraphics[keepaspectratio, scale=0.7]{figure/mag_move.eps}](img8.png)
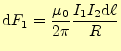
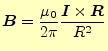
![\includegraphics[keepaspectratio,scale=0.7]{figure/Amper_force.eps}](img25.png)