[Previous: 1 概要] [Up: 矩形導波管中の電磁波の減衰] [Next: この文書について...]
摂動計算により表面近くの電場を計算して, ポインティングベクトルの計算を行うことに する. 金属の抵抗は非常に小さく, マイクロ波は完全反射すると仮定しても, ほとんどの 場合問題ない. 完全反射だとロスが生じないので, 完全反射の磁場から有限の小さい抵抗 があった場合の, 金属表面の電場を求める.
金属中の電磁場の振る舞いを示す方程式は,
完全導体の境界条件の場合, 磁場は金属の接線方向のみで, 電流はその垂直方向に流れて いる. この場合, 電流の厚さは無限小で, 無限大の電流密度となる. しかし, 抵抗が無い ので, 電流が流れていても, それによる電場は無い. 一方, 有限な抵抗を有する金属では 図のように電流分布が厚さ方向に広がっており, 電流の方向に電場もある.
表面に垂直の電場は許されるが, それには興味がないのでここでは図に書いていない. な ぜならば, 表面に垂直な電場と図にかかれている磁場が作るポインティングベクトルは, 金属に沿って流れるため, マイクロ波のロスにならないからである.
興味の対象は, 金属の中に向かっているポインティングベクトルである. ロスを計算する
上で重要なものは, 図に示している空気と金属の境界でのx方向の磁場とそれに垂直なz方
向の電場である. 完全導体であればz方向の電場は存在しないが, 有限な抵抗を
持つ金属では, 磁場を作る電流により電場が発生する. その電場は,
![]() という関係を満たす.
という関係を満たす.
この電場は, 高周波の電場, 式(3)と異なることに
注意が必要である. 高周波の電場は, ![]() 方向を向いており, ポインティングベクトルは
方向を向いており, ポインティングベクトルは
![]() 方向を向くため, 導波管での電磁波の減衰にはならないのは以前に述べたとおりであ
る. ここで問題としているのは, 磁場を作るための電流が流れるとできる電場である. い
わゆるオーム損失である.
方向を向くため, 導波管での電磁波の減衰にはならないのは以前に述べたとおりであ
る. ここで問題としているのは, 磁場を作るための電流が流れるとできる電場である. い
わゆるオーム損失である.
図2の様な座標系の元, 式(10)を計算し
て, 磁場を作る電流による電場を計算するのである.式(10)はベク
トルの方程式であるが, 図に示すように座標系と決めれば, ![]() のみのスカラーの方程
式になる. この式を解くことになるが, そのままでは, 計算が大変である. そこで, 左辺
のフーリエ成分のみ考え, 電場は
のみのスカラーの方程
式になる. この式を解くことになるが, そのままでは, 計算が大変である. そこで, 左辺
のフーリエ成分のみ考え, 電場は![]() しかないことを忘れないで, 計算すると
しかないことを忘れないで, 計算すると
| 左辺 | 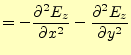 |
(11) |
| (12) |
![[*]](crossref.png) )のう
ち,
)のう
ち, | (13) |
| (14) |
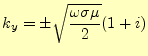 |
(15) |
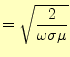 |
(16) |
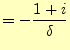 |
(17) |
|
これまでの![]() の計算結果から, 金属中深さ方向の電場の強度分布がわかる. 即ち,
の計算結果から, 金属中深さ方向の電場の強度分布がわかる. 即ち,
金属表面(y=0)での電場は![]() で, 磁場は
で, 磁場は![]() とすると, その関係を導く必要がある.
そのために, 式(6)を使うことにする. ただ, 表
とすると, その関係を導く必要がある.
そのために, 式(6)を使うことにする. ただ, 表![[*]](crossref.png) に示すように, 変位電流の項は無視できるので,
に示すように, 変位電流の項は無視できるので,
| (19) |
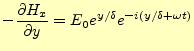 |
(20) |
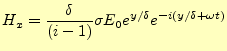 |
(21) |
 |
(22) |
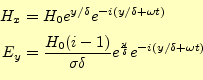 |
これから, 金属表面でのポインティングベクトルを計算すれば, 磁場![]() の時のロスが
分かる. 1周期にわたって積分して, その平均のポインティングベクトルの大きさは,
の時のロスが
分かる. 1周期にわたって積分して, その平均のポインティングベクトルの大きさは,
となる. これで, ![]() をパラメーターとして, 導波管を通過するマイクロ波の電力が分
かった.
をパラメーターとして, 導波管を通過するマイクロ波の電力が分
かった.
次に必要な計算は, 導波管のトータルのロスである. 式(24)を導波管の 壁に沿って積分する. すると,
これから単位長さあたりの減衰量![]() [dB/m]を計算する. この
[dB/m]を計算する. この![]() の定義は次の
ようになる.
の定義は次の
ようになる.
| (27) |