...山本昌志 ¹

国立秋田工業高等専門学校　電気情報工学科

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...曲面はそれぞれ直交²

斜向座標系はここでは取り 扱わない。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...はクロネッカー記号 ³

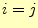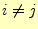$i=j$のとき1、$i\neq j$のとき0の値をとる。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...は一般化座標⁴

解析 力学の一般化座標と似ているので、ここではそう呼んだ。実際にはこのように呼ばない。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...微少変位させた軌跡で作られる平行四辺形 ⁵

直交しているので、長方形である。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...#tex2html_wrap_inline3576#
⁶

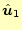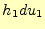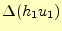変位ベクトルの $\hat{\boldsymbol{u}}_1$方向の成分は、$h_1du_1$である。 $\Delta(h_1u_1)$とならないことに 注意。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... フラックス⁷

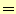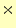面の法線方向からでるベクトル場の総量。フラックス$=$(面積) $\times$(面の法線方向のベクトル)である。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...方向成分 ⁸

成分は内積を計算すれば、求められる。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.