3 座標系の変換

ベクトル場の微分を考えるとき、位置ベクトルが重要な役割を果たす。この位置ベクトル の取り扱いについて、ここでは述べる。特に、スケール因子が座標系の変換の中心的な役 割を果たすことに注意しよう。それは、座標系を変えて積分をするときのヤコビ行列と同 じような働きをする。

以降の議論では、カーテシアン座標系と曲線座標系の関係について述べる。ここで取り扱 う曲線座標系は直交座標系に限る。曲線座標系と言っても、おなじみの円筒座標系や極座 標系のことである。これ以外にもいろいろな、直交曲線座標系はある。

カーテシアン座標系は特別な座標系ではなく、直交曲線座標系のひとつと考えられるが、 特別に良い性質がある。それは、線素や面積素、体積素がすぐにわかることである。その ため、カーテシアン座標系と曲線座標系を比較して、必要な諸量を計算する。

3.1 位置ベクトル

3次元空間の任意の点の位置はカーテシアン座標系で$(x,y,z)$と表すことができる。この 3つの数値で表された量はベクトル量で、位置ベクトルといわれる。同じ位置ベクトルを、 曲線座標系では、 $(u_1, u_2,u_3)$と表すことにする。当然、カーテシアン座標系の成分 $x,y,z$は、

$$\begin{aligned}x=x\left(u_1,u_2,u_3\right)\\ y=y\left(u_1,u_2,u_3\right)\\ z=z\left(u_1,u_2,u_3\right) \end{aligned}$$

と $u_1, u_2, u_3$を独立変数とした関数で表すことができる。逆もまた然りである。

$$\begin{aligned}u_1=u_1\left(x,y,z\right)\\ u_2=u_2\left(x,y,z\right)\\ u_3=u_3\left(x,y,z\right) \end{aligned}$$

これら(3)(4)式は、特別なことを言っている のではなく、ある直交座標系の位置ベクトルの成分 $(u_1, u_2, u_3)$が決まれば、カー テシアン座標系のそれ$(x,y,z)$が一意に決まると言っているにすぎない。また逆も、同 様に成り立つ。今までの経験でよく知っていることである。たとえば、ある任意 の点は、極座標の $(r,\theta,\phi)$で表現しても、カーテシアン座標で表現しても、一 意に表すことができる。

要するに3次元座標系の位置ベクトルは、3個の数値で表すことができるのである。その３ 個の数値と取り方は、座標系に依存する。そして、それらには1対1の関係がある。

先に述べたように、ここでは直交曲線座標を取り扱う。したがって、ここで述べている曲 線座標系 $(u_1,u_2,u_3)$のお互いの軸は、直交することになる。さらに、ここでは通常 使われる右手系のみを取り扱うことにする。

3.2 単位ベクトル

今後の議論として、もう一つ準備が必要である。単位ベクトルを定義する。普通、カーテ シアン座標系では、それらは $\boldsymbol{i}, \boldsymbol{j}, \boldsymbol{k}$と表現される。そうすると、位置ベク トル $\boldsymbol{r}$は

$$\boldsymbol{r}=x\boldsymbol{i}+y\boldsymbol{j}+z\boldsymbol{k}$$ (5)

となる。カーテシアン座標系の場合、位置を表す$(x,y,z)$が位置ベクトルの成分になる。 一方、曲線座標系で使う単位ベクトルを $\hat{\boldsymbol{u}}_1,\hat{\boldsymbol{u}}_2,\hat{\boldsymbol{u}}_3$とすると

$$\boldsymbol{r}\neq u_1\hat{\boldsymbol{u}}_1+u_2\hat{\boldsymbol{u}}_2+u_3\hat{\boldsymbol{u}}_3$$ (6)

となる。曲線座標系での位置は、 $(u_1,u_2,u_3)$で表せるが、それはそこで使う単位ベ クトルの成分とならないのである。これが曲線座標系を使う場合の面倒くさい部分である が、しょうがない。これ以降、この面倒な部分の取り扱いを延々と示すことになる。

まずは、基底となる単位ベクトルを定義しておく必要がある。カーテシアン座標系と極座標系 (曲線座標系)の単位ベクトルを図2と 3に示す。これをみながら、以下の説明を理解してほしい。ま ずわかりやすい、カーテシアン座標系からである。単位ベクトル $\boldsymbol{i}$は、位置ベクト ルの$x$成分を固定し、$y$,$z$ をパラメーターとした$yz$平面に垂直で、$x$が増加する 方向に向いている。従って、単位ベクトル $\boldsymbol{i}$は$x$軸に平行で、$x$が増加する方向 に向いている。その大きさは1である。他の単位ベクトル、 $\boldsymbol{j}$や $\boldsymbol{k}$も同じよ うに説明できる。$xy$、$yz$、$zx$平面の法線はそれぞれ直交しているので、単位ベクト ル $\boldsymbol{i},\boldsymbol{j},\boldsymbol{k}$もそれぞれ直交している。曲線座標でも事情は同じである。ベ クトル $\hat{\boldsymbol{u}}_1$は、$u_1$成分を固定し、$u_2$,$u_3$ をパラメーターとした $u_2u_3$曲面に垂直で、$u_1$が増加する方向に向いている。さらに、それぞれの曲面、 $u_1u_2$、$u_2u_3$、$u_3u_1$曲面はそれぞれ直交²しているので、単位ベクトル同士も直交している。これらの単位ベクトルが 直交していることと、大きさが1であることは、

$$\hat{\boldsymbol{u}}_i\cdot\hat{\boldsymbol{u}}_j=\delta_{ij}$$ (7)

と表すことができる。ここで、 $\delta_{ij}$はクロネッカー記号 ³である。 で表せる。

カーテシアン座標系と曲面座標系の単位ベクトルはよく似ているが、大きな違いがある。 それは、カーテシアン座標系ではどの位置でも単位ベクトルは同じであるが、曲面座標で は座標により単位ベクトルは異なる。このことが曲面座標を使うことの数学的な取り扱い を難しくしている。ただ、この取り扱いが少し難しくなる不利益よりも、多大な利益を得 ることができることがあるため、曲線座標が使われることが多い。

最後にひとつ注意を与えておく。これまではカーテシアン座標$(x,y,z)$と他の直交座標 系 $(u_1, u_2, u_3)$を分けて話した。しかし、カーテシアン座標系も直交座標系の一つ であるため、$x,y,z$を $u_1,u_2,u_3$に置き換えても良い。置き換えかたも任意に決めて 良いのである。

ただし、ここでは右手系と取り扱うことにしたので、

$$\begin{aligned}\hat{\boldsymbol{u}}_1=\hat{\boldsymbol{u}}_2\ti... ...=\hat{\boldsymbol{u}}_1\times\hat{\boldsymbol{u}}_2 \end{aligned}$$

の関係を満たすように曲線座標系は決めなくてはならない。

図 2: カーテシアン座標系

図 3: 極座標系

3.3 接ベクトル

ここでは、接ベクトルを導入して、曲線座標の変化と位置ベクトルの変化の関係を求める。 要するに、座標が $(du_1,du_2,du_3)$変化した場合の位置ベクトルの変化 $d\boldsymbol{r}$を知 りたいのである。カーテシアン座標系の場合は、これは簡単で、

$$d\boldsymbol{r}=\boldsymbol{i}dx+\boldsymbol{j}dy+\boldsymbol{k}dz$$ (9)

である。しかし、曲線座標系の場合、このように簡単にならず、

$$d\boldsymbol{r}\neq\hat{\boldsymbol{u}}_1du_1+\hat{\boldsymbol{u}}_2du_2+\hat{\boldsymbol{u}}_3du_3$$ (10)

である。座標の変化が位置ベクトルの成分の変化とならないのである。これらのことは、 式(5)や(6)から直ちに分かる。

曲線座標系の位置ベクトルの変化を考える。そのために、よく分かっているカーテシアン 座標系の式(3)から始め、曲線座標系に移る。この式の位置ベクト ルの全微分は、

$$d\boldsymbol{r} =\left(dx,dy,dz\right)$$

$$= \left( \if 11 \frac{\partial x}{\partial u_1} \else \frac{\part... ... z}{\partial u_3} \else \frac{\partial^{1} z}{\partial u_3^{1}}\fi du_3 \right)$$ (11)

となる。この式は、曲線座標系を $(du_1,du_2,du_3)$と変化させた場合、カー テシアン座標系での位置ベクトルの変化を表している。

ここで、曲線座標の変化を $(du_1,0,0)$とした場合を考える。このとき、位置ベクトルの 変位 $d\boldsymbol{r}$は、$u_2u_3$に曲面の法線方向に向いているのは明らかであろう。従って、 $u_1$曲線に接していることになる。この変位はベクトルで、単位ベクトル $\hat{\boldsymbol{u}}_1$と平行になるのも明らかであろう。曲線座標の変化を $(du_1,0,0)$とし た場合の変位ベクトル $d\boldsymbol{r}_1$は、式(11)を用いて計算すると

$$d\boldsymbol{r}_1 =\left( \if 11 \frac{\partial x}{\partial u_1} \else \frac{\parti... ... z}{\partial u_1} \else \frac{\partial^{1} z}{\partial u_1^{1}}\fi du_1 \right)$$

$$=\left( \if 11 \frac{\partial x}{\partial u_1} \else \frac{\parti... ...l z}{\partial u_1} \else \frac{\partial^{1} z}{\partial u_1^{1}}\fi \right)du_1$$

$$=\left( \if 11 \frac{\partial x}{\partial u_1} \else \frac{\parti... ..._1} \else \frac{\partial^{1} z}{\partial u_1^{1}}\fi \boldsymbol{k} \right)du_1$$ (12)

となる。これは、座標が$du_1$変化した場合の位置ベクトルの変位を表している。同じこ とが、$du_2$や$du_3$についても言える。

式(12)の右辺の括弧内のベクトルは、接ベクトルと呼ばれている。 接ベクトルは、それぞれの変位に対して決められ、

$$\begin{aligned}\boldsymbol{U}_1&= \if 11 \frac{\partial x}{\par... ...\partial^{1} z}{\partial u_3^{1}}\fi \boldsymbol{k} \end{aligned}$$

となる。一般的に書けば、

$$\boldsymbol{U}_i = \if 11 \frac{\partial x}{\partial u_i} \else \frac{\partial^{1}... ...}{\partial u_i} \else \frac{\partial^{1} z}{\partial u_i^{1}}\fi \boldsymbol{k}$$ (14)

である。これから、曲線座標が $(du_1,du_2,du_3)$変わると位置ベクトルの変位は、

$$d\boldsymbol{r}=\boldsymbol{U}_1du_1+\boldsymbol{U}_2du_2+\boldsymbol{U}_3du_3$$ (15)

である。これで、この節の目的である曲線座標の変化と位置ベクトルの変化の関係を求め ることができた。

3.4 スケール因子

曲線座標の変化と位置ベクトルの変化の関係は、前節の式 (15)で示した。この場合、接ベク トルと言うやっかいなものがある。ここでは、スケール因子を用いて、それらの関係をも う少し分かりやすく表現する。

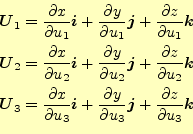前節に述べたように、接ベクトルと単位ベクトルの方向は一致している。そのため、

$$\boldsymbol{U}_i=h_i\hat{\boldsymbol{u}}_i$$ (16)

とする事ができる。接ベクトルと単位ベクトルをつなぐ定数$h_i$をスケール因子と言 う。このスケール因子は、 $h_1,h_2,h_3$と3個の数で表すことができるが、ベクトルでは ない。スケール因子を使うと、位置ベクトルの変位は、

$$d\boldsymbol{r}_i=h_i\hat{\boldsymbol{u}}_idu_i$$ (17)

と表すことができる。座標が $(du_1,du_2,du_3)$変位したときの位置ベクトルの微少変位 は、

$$d\boldsymbol{r}= h_1\hat{\boldsymbol{u}}_1du_1+h_2\hat{\boldsymbol{u}}_2du_2+h_3\hat{\boldsymbol{u}}_3du_3$$ (18)

となる。これは、スケール因子を用いることにより、座標の変化から、直接位置ベクトル の変化を示す式が得られることを示している。従って、曲線座標の位置ベクトルの変位を 計算するためにはスケール因子の計算が重要となる。

ここで定義したスケール因子の中には、接ベクトルが隠れているので、前節の内容 と矛盾しないばかりか、同じである。それにも関わらず、接ベクトルではなくスケール 因子を使のは、

• 変位ベクトルを表す式の内容がわかりやすくなる。スケール因子と言うように座標 のスケールの変換を使っているように考え方を変えるメリットは計り知れない。

からである。このスケール因子は座標の変化に対してのスケールである。基準はカーテシ アン座標である。また、絶対位置のスケールでないことに注意しておく。座標を表す3個 の量の一つを$du_i$と変化させると、座標ベクトルは $h_i\hat{\boldsymbol{u}}_idu_i$と変わる のである。これは、カーテシアン座標系で、$dx$変化させると、位置ベクトルが $\boldsymbol{i}dx$変化するのと同じである。後で述べるが、カーテシアン座標系のスケール因子 は1である。

残った問題は、スケール因子を求める具体的な方法である。それを導くために、式 (16)の両辺を2乗し、式(14)を代入す ると

$$h_i^2 =U_i^2$$

$$=\left( \if 11 \frac{\partial x}{\partial u_i} \else \frac{\parti... ...ial z}{\partial u_i} \else \frac{\partial^{1} z}{\partial u_i^{1}}\fi \right)^2$$ (19)

が得られる。これが、スケール因子を求める公式である。曲線座標系のスケール因子を求 めるためにはカーテシアン座標系と比較することになる。なにしろ、カーテシアン座標系 のスケールは直感で分かるように非常に簡単なのであるため、それと比較することになる。

式(16)の示すところをみると、スケール因子の2乗の計算は 簡単である。すると、スケール因子そのものは、その$1/2$乗を計算すれば良いのである が、符号の問題が残る。これは、スケール因子を決めている式(16) を考えればよい。一般には、単位ベクトル $\hat{\boldsymbol{u}}_i$の方向は、$du_i$を増加させ た方向とする。従って、$h_i$は正の値となる。

この結果をみてわかるように、$h_idu_i$は変位ベクトルの大きさを示し、長さの次元に なる。$u_i$は長さの次元である必要はなく、角度等を用いて座標を表すことができるが、 スケール因子を乗じると長さの次元になるのである。$u_i$は一般化座標⁴とでも言うもので、スケール因子を乗じることにより長さの次元のおなじみの座標になる。 スケール因子と言う名前はその働きを、よく表している。

もっとよくスケール因子のイメージが湧くのは、座標を$d_i$のみ変化させた場合である。 その場合の座標の変化(距離)を$ds_i$とすると

$$ds_i=h_idu_i$$ (20)

となる。これは、実にわかりやすい。実際の長さの変化は、座標を表すパラメーターの変 化にスケール因子をかければよいのである。まずこのイメージをつかむことが重要である。

表1に、実際の問題でよく使われる3つの座標系について、スケー ル因子を示す。これを求める手順は簡単で、次のようにする。

1. 問題に適した直交曲線座標系を決めて、カーテシアン座標系との関係をもとめる。
2. 式(19)に従い、スケール因子を計算する。

表 1: 電磁気学でよく使われる座標系。一般座標、カーテシアン座標系との関係、 スケール因子を示している。

	座標系
	カーテシアン	円柱	極
座標系イラスト	図4	図5	図6
$(u_1,u_2,u_3)$	$(x,y,z)$	$(r,\theta,z)$	$(r,\theta,\varphi)$
$x$	$x$	$r\cos\theta$	$r\sin\theta\cos\varphi$
$y$	$y$	$r\sin\theta$	$r\sin\theta\sin\varphi$
$z$	$z$	$z$	$r\cos\theta$
$h_1$	$1$	$1$	$1$
$h_2$	$1$	$r$	$r$
$h_3$	$1$	$1$	$r\sin\theta$

ここで示した曲線座標系とはことなるものについても、同じような方法でスケール因子を 求めることができるので、必要に応じて計算すればよい。

図 4: カーテシアン座標系

図 5: 円柱座標系

図 6: 極座標系

ホームページ: Yamamoto's laboratory
著者: 山本昌志