ここでは、曲線座標系での微分演算子について、説明する。なんと言ってもよく使われる
微分演算子は、勾配と発散、回転である。カーテシアン座標系では、これらの表現は簡単
であるが、曲線座標系ではどうなるだろうか?。いろいろな方法で曲線座標系のこれらの
微分演算子を導出することができるが、これまでに求めたスケール因子を使うと非常に簡
単でわかりやすい。
スカラー場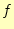 の勾配
の勾配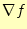 は、
は、
と定義できる。座標を
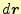 変化させると、スカラー場の値は
変化させると、スカラー場の値は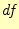 変わるので
ある。スカラー場の変化は、勾配に座標の変化量の内積である。スカラー場の変化量はス
カラー量、座標の変化はベクトル量であるため、勾配はベクトル量である。勾配の方向は、
式(28)から分かるように、スカラー場の正の変化量が最大の方向で
ある。内積は、各々のベクトルの大きさと、それらのなす角の余弦を乗じた値になるから
である。
変わるので
ある。スカラー場の変化は、勾配に座標の変化量の内積である。スカラー場の変化量はス
カラー量、座標の変化はベクトル量であるため、勾配はベクトル量である。勾配の方向は、
式(28)から分かるように、スカラー場の正の変化量が最大の方向で
ある。内積は、各々のベクトルの大きさと、それらのなす角の余弦を乗じた値になるから
である。
ここで、曲線座標系の微少変位ベクトル
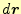 は、式(18)
に示されている。これが、式(28)が右辺の
は、式(18)
に示されている。これが、式(28)が右辺の
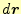 の項になる。次に、勾
配
の項になる。次に、勾
配
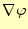 はベクトル量なので、係数
はベクトル量なので、係数
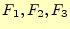 を使って、
を使って、
と表すことができる。この式の
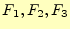 を求めることができれば、曲線座標系の勾
配が分かる。そのために、これと式(18)を
式(28)に代入すると
を求めることができれば、曲線座標系の勾
配が分かる。そのために、これと式(18)を
式(28)に代入すると
となる。
一方、スカラー場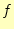 は位置の関数であるため、独立変数
は位置の関数であるため、独立変数
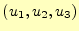 を使って、
を使って、
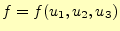 |
(31) |
と書くことができる。この関数の全微分は、
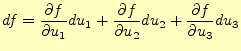 |
(32) |
である。この結果と式(30)を比べると、
となる。これから
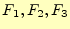 を求め、式(29に代入する
と、曲線座標系の勾配が
を求め、式(29に代入する
と、曲線座標系の勾配が
と求められる。これで、この節の目的である、曲線座標系の勾配を求める式を得ることが
できた。
この式の解釈は簡単で、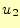 と
と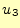 を固定して
を固定して
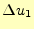 変化させた場合の
変化させた場合の
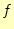 の変化は、
の変化は、
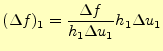 |
(35) |
となる。ここで、
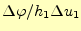 6の極限の操作をおこなうと、これは
6の極限の操作をおこなうと、これは
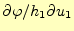 となる。
となる。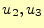 を固定しているので偏
微分になるのである。この偏微分が
を固定しているので偏
微分になるのである。この偏微分が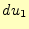 のみを変化させたときのスカラー場
のみを変化させたときのスカラー場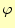 の変化
率、即ち、勾配の
の変化
率、即ち、勾配の
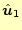 方向成分である。ちょうど、式(34)の
右辺の第1項である。
方向成分である。ちょうど、式(34)の
右辺の第1項である。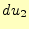 や
や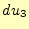 も同様である。ここでも、スケール因子が重要な役
割を果たしている。
も同様である。ここでも、スケール因子が重要な役
割を果たしている。
おまけとして、7.1節に、非常に危なっかしい方法でこの勾配の
求め方を示す。
ベクトル場
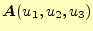 の発散
の発散
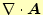 は、ある体積要素から流れ出る
フラックス7の総量をその体積で割ることにより求めら
れる。これは、スカラー量になる。例えば、図7のようにベクトル場に閉
じた領域を考え、その表面から流れ出るフラックスの総量を体積で割るのである。体積要
素をどんどん小さくすると、形状に依存しないである値に近づく。そして、この体積要素
をゼロにした極限が発散と定義できる。これを式で表すと、
は、ある体積要素から流れ出る
フラックス7の総量をその体積で割ることにより求めら
れる。これは、スカラー量になる。例えば、図7のようにベクトル場に閉
じた領域を考え、その表面から流れ出るフラックスの総量を体積で割るのである。体積要
素をどんどん小さくすると、形状に依存しないである値に近づく。そして、この体積要素
をゼロにした極限が発散と定義できる。これを式で表すと、
となる。ここで、分母は体積となり、分子は表面積とその法線方向のベクトル場の積分と
なる。これは、分母分子の極限を計算しているので、ベクトル場の微分となっている。
それでは、曲線座標系の微少体積要素を用いて、その微分の内容を求めてみよう。微少体
積要素は局面からなる6面体で、図8のようになっている。この微少体積要素
のベクトル場の変化やスケール因子の変化をよく考えて、発散を求める。式
(36)を全て計算するのは紙面の都合上厳しいので、まずは
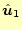 方向のフラックスを計算する。図でも分かるように、ベクトル場
方向のフラックスを計算する。図でも分かるように、ベクトル場
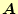 の
の
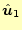 方向成分
8
方向成分
8
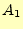 は、一方の面では入り込み、他方では出ている。さらに、この2面で、ベクトル
は、一方の面では入り込み、他方では出ている。さらに、この2面で、ベクトル
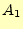 の値とスケール因子の値が異なることに注意が必要である。
の値とスケール因子の値が異なることに注意が必要である。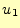 の面でのそれぞれ
の値を
の面でのそれぞれ
の値を
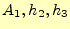 とすると、
とすると、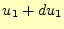 でのそれらは、
でのそれらは、
となる。フラックスは面積とベクトルの成分の積なので、この2面の寄与は
となる。ここでは丁寧に計算したが、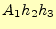 で一つの関数と考え
で一つの関数と考え
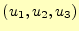 を
独立変数と考えれば、もっと簡単に式(40)を求めることができる。即ち、
この関数の一次の変化量は、
を
独立変数と考えれば、もっと簡単に式(40)を求めることができる。即ち、
この関数の一次の変化量は、
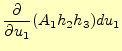 |
(41) |
となる。これに、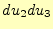 を乗算すれば、式(40)と同じ結果が得られる。
を乗算すれば、式(40)と同じ結果が得られる。
残りの面に関しても、式(40)を
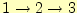 の順にサイ
クリックに入れ替えれば求めることができる。これらの全てのフラックスを合計して、局
面座標の微少体積要素で式(36)を考えると
の順にサイ
クリックに入れ替えれば求めることができる。これらの全てのフラックスを合計して、局
面座標の微少体積要素で式(36)を考えると
となる。これが、局面座標系の発散を求める式である。
|
図 8:
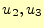 面での発散 面での発散
|
|
|
ベクトル場
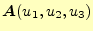 の回転
の回転
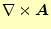 は、面積要素の縁のベクトルの
線積分をその面積で割ることにより求められる。これは、面の法線方向に向かったベクト
ル量となる。図9のように計算する面は任意で、値はその放線方向のベク
トルの成分となる。通常は、計算が便利な、
は、面積要素の縁のベクトルの
線積分をその面積で割ることにより求められる。これは、面の法線方向に向かったベクト
ル量となる。図9のように計算する面は任意で、値はその放線方向のベク
トルの成分となる。通常は、計算が便利な、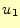 あるいは
あるいは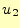 、
、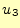 が一定のそれぞ
れの面で計算する。図10に示すように、3つの面が交わるところが、
が一定のそれぞ
れの面で計算する。図10に示すように、3つの面が交わるところが、
 の位置を示し、その曲面の微少面で回転を計算する。そして、計算され
た回転の成分は、この曲面の法線方向で表すことができる。例えば、図9
のように
の位置を示し、その曲面の微少面で回転を計算する。そして、計算され
た回転の成分は、この曲面の法線方向で表すことができる。例えば、図9
のように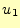 が一定の曲面の閉じた領域を考える。ここで、その領域の縁のベクトルを
線績分してその面積で割るのである。面積要素をどんどん小さくすると、形状に依存しな
いである値に近づく。この一定の値が、ベクトル場の回転の
が一定の曲面の閉じた領域を考える。ここで、その領域の縁のベクトルを
線績分してその面積で割るのである。面積要素をどんどん小さくすると、形状に依存しな
いである値に近づく。この一定の値が、ベクトル場の回転の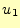 方向成分である。これ
は、
方向成分である。これ
は、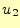 、
、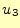 一定のそれぞれの面で考えることができるので、ベクトル場のある点で
3成分の値を持つことになる。そして、これはベクトル量になる。これが、ベクトル場の
回転である。これを式で表すと、
一定のそれぞれの面で考えることができるので、ベクトル場のある点で
3成分の値を持つことになる。そして、これはベクトル量になる。これが、ベクトル場の
回転である。これを式で表すと、
となる。ここで、分母は面積となり、分子は面の縁の接線方向のとベクトル場の線積分と
なる。これもまた、分母/分子の極限を計算しているので、ベクトル場の微分となっている。
発散のときと同様に、曲線座標系の微少面積要素を用いて、その微分の内容を求めてみよ
う。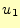 が一定の場合の微少体面積要素は、
が一定の場合の微少体面積要素は、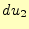 と
と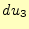 からなる面で、図
11のようになっている。ベクトル場の変化やスケール因子の変化をよく考え
て、回転を求める。式(43)の
からなる面で、図
11のようになっている。ベクトル場の変化やスケール因子の変化をよく考え
て、回転を求める。式(43)の
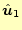 方向の成分を計算
することにする。この式の右辺の分母の面積要素は、式(24)で示さ
れているので、回転の総量を表す分子の計算を行う。これは、反時計回りにベクトル場の
接線成分を線積分することにより求められる。図から分かるように、ベクトル場
方向の成分を計算
することにする。この式の右辺の分母の面積要素は、式(24)で示さ
れているので、回転の総量を表す分子の計算を行う。これは、反時計回りにベクトル場の
接線成分を線積分することにより求められる。図から分かるように、ベクトル場
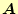 の
の
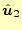 方向成分
方向成分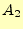 は、一方の辺では積分の方向と同じで、対向する辺で
は逆になる。また、この2辺ではで、ベクトル
は、一方の辺では積分の方向と同じで、対向する辺で
は逆になる。また、この2辺ではで、ベクトル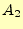 の値の他にスケール因子の値も異なる
ことに注意する事は発散のの計算と同じである。
の値の他にスケール因子の値も異なる
ことに注意する事は発散のの計算と同じである。
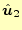 方向の
方向の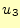 での、そ
れぞれの値を
での、そ
れぞれの値を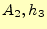 (図11の右の辺) とすると、
(図11の右の辺) とすると、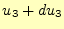 でのそれらは、
でのそれらは、
となる。従って、この2面(図の右と左の辺)の回転の寄与は、
となる。符号に気をつけて、同様のことを図11の上と下の辺で行うと、そこ
での回転の総量は
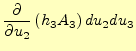 |
(47) |
となる。以上より、上下左右のすべての辺の線積分がわかった。面積要素は、
 と分かっている。これから、線積分を面積で割った
と分かっている。これから、線積分を面積で割った
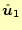 方
向の回転は
方
向の回転は
となる。残りの2成分は、成分を表す記号を
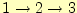 とサイクリック
に変えれば求められる。従って、回転は
とサイクリック
に変えれば求められる。従って、回転は
となる。ただ、この式は長くて憶えにくい。そこで、通常は、
とする事が多い。
図 11:
 面での発散
面での発散
|
|
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成20年3月24日
![]() は、式(18)
に示されている。これが、式(28)が右辺の
は、式(18)
に示されている。これが、式(28)が右辺の
![]() の項になる。次に、勾
配
の項になる。次に、勾
配
![]() はベクトル量なので、係数
はベクトル量なので、係数
![]() を使って、
を使って、
![]() は位置の関数であるため、独立変数
は位置の関数であるため、独立変数
![]() を使って、
を使って、
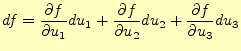
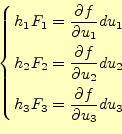
![]() と
と![]() を固定して
を固定して
![]() 変化させた場合の
変化させた場合の
![]() の変化は、
の変化は、
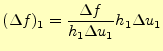
![]() 方向のフラックスを計算する。図でも分かるように、ベクトル場
方向のフラックスを計算する。図でも分かるように、ベクトル場
![]() の
の
![]() 方向成分
8
方向成分
8
![]() は、一方の面では入り込み、他方では出ている。さらに、この2面で、ベクトル
は、一方の面では入り込み、他方では出ている。さらに、この2面で、ベクトル
![]() の値とスケール因子の値が異なることに注意が必要である。
の値とスケール因子の値が異なることに注意が必要である。![]() の面でのそれぞれ
の値を
の面でのそれぞれ
の値を
![]() とすると、
とすると、![]() でのそれらは、
でのそれらは、
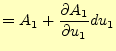

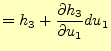
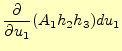
![]() の順にサイ
クリックに入れ替えれば求めることができる。これらの全てのフラックスを合計して、局
面座標の微少体積要素で式(36)を考えると
の順にサイ
クリックに入れ替えれば求めることができる。これらの全てのフラックスを合計して、局
面座標の微少体積要素で式(36)を考えると
![]() が一定の場合の微少体面積要素は、
が一定の場合の微少体面積要素は、![]() と
と![]() からなる面で、図
11のようになっている。ベクトル場の変化やスケール因子の変化をよく考え
て、回転を求める。式(43)の
からなる面で、図
11のようになっている。ベクトル場の変化やスケール因子の変化をよく考え
て、回転を求める。式(43)の
![]() 方向の成分を計算
することにする。この式の右辺の分母の面積要素は、式(24)で示さ
れているので、回転の総量を表す分子の計算を行う。これは、反時計回りにベクトル場の
接線成分を線積分することにより求められる。図から分かるように、ベクトル場
方向の成分を計算
することにする。この式の右辺の分母の面積要素は、式(24)で示さ
れているので、回転の総量を表す分子の計算を行う。これは、反時計回りにベクトル場の
接線成分を線積分することにより求められる。図から分かるように、ベクトル場
![]() の
の
![]() 方向成分
方向成分![]() は、一方の辺では積分の方向と同じで、対向する辺で
は逆になる。また、この2辺ではで、ベクトル
は、一方の辺では積分の方向と同じで、対向する辺で
は逆になる。また、この2辺ではで、ベクトル![]() の値の他にスケール因子の値も異なる
ことに注意する事は発散のの計算と同じである。
の値の他にスケール因子の値も異なる
ことに注意する事は発散のの計算と同じである。
![]() 方向の
方向の![]() での、そ
れぞれの値を
での、そ
れぞれの値を![]() (図11の右の辺) とすると、
(図11の右の辺) とすると、![]() でのそれらは、
でのそれらは、
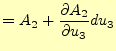
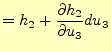
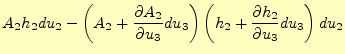
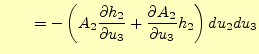
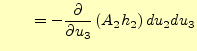
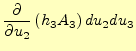
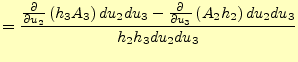
![$\displaystyle =\frac{1}{h_2h_3}\left[ \frac{\partial}{\partial u_2}\left(h_3A_3\right) -\frac{\partial}{\partial u_3}\left(A_2h_2\right) \right]$](img313.png)
![$\displaystyle \frac{1}{h_2h_3}\left[ \frac{\partial}{\partial u_2}\left(A_3h_3\...
...-\frac{\partial}{\partial u_3}\left(A_2h_2\right) \right]\hat{\boldsymbol{u}}_1$](img316.png)
![$\displaystyle \frac{1}{h_3h_1}\left[ \frac{\partial}{\partial u_3}\left(A_1h_1\...
...-\frac{\partial}{\partial u_1}\left(A_3h_3\right) \right]\hat{\boldsymbol{u}}_2$](img318.png)
![$\displaystyle \frac{1}{h_1h_2}\left[ \frac{\partial}{\partial u_1}\left(A_2h_2\...
...-\frac{\partial}{\partial u_2}\left(A_1h_1\right) \right]\hat{\boldsymbol{u}}_3$](img320.png)