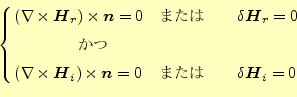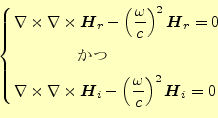ここでは、マクスウェルの方程式から電磁場が満たす波動方程式を導き、それが満たす汎
関数を示す。
このあたりの説明は、以前示したヘルムホルツ方程式
の話とほとんど同じである。ただ、汎関数の計算に便利なようにちょっとだけ偏微分方程
式の形を変えているのと、計算過程が少し異なる。本質的には全く同じである。
ここでは軸対称構造の共振空洞内の共振モードの電磁場の方程式を示す。この場合、内部
は真空で、金属で囲まれた空間になる。当然、ここの電磁場はマクスウェルの方程式で記
述される。ただし、内部には電荷も電流が無いという条件が付される。マクスウェルの方
程式で、
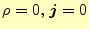 となる。
となる。
また、誘電率と透磁率は一定で、それぞれ
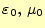 となる。そして、
となる。そして、
の関係がある。式(1)〜(4)は、連立の偏微
分方程式なので、計算しやすい形に直すことにする。
まずは、磁場の方程式を求めることにする。そのために、式(4)の両辺
に回転の演算子を作用させる。そうすると、
となる。これは、波動方程式である。電磁波の速度は光速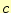 で、この方程式では
で、この方程式では
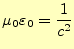 |
(8) |
となる。従って、磁場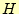 が満たす方程式は、
が満たす方程式は、
となる。
この式も、場所と時間の両方の項の偏微分方程式なので、解くのは面倒である。
そのため、
と変数分離ができるか考える。通常、変数分離はできるか否かは分からないので、とりあ
えずやってみることにする。式(10)を(9)に入
れると
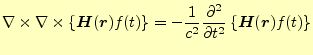 |
(11) |
となり、時間と空間の微分を考えると
となる。以降、簡素に記述するために、磁場の空間の関数を
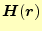 は
は
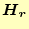 と、時間の関数
と、時間の関数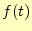 は
は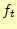 とする。ここで、変数分離のいつものパター
ンで、左辺と右辺に、時間及び空間のみ関数にしたいわけだが、ベクトルの演算なので少
し気をつける。そのため、この式の両辺に
とする。ここで、変数分離のいつものパター
ンで、左辺と右辺に、時間及び空間のみ関数にしたいわけだが、ベクトルの演算なので少
し気をつける。そのため、この式の両辺に
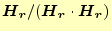 なるベクトルの
内積の演算を施す。すると
なるベクトルの
内積の演算を施す。すると
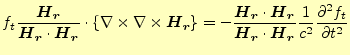 |
(13) |
となる。これを整理すると、
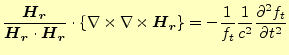 |
(14) |
である。この偏微分方程式は、左辺は空間
 、右辺は時間
、右辺は時間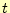 のみの関数である。
それぞれ別の独立変数となっているので、この等式が成り立つためには、その値は定数で
なくてはならない。この定数を
のみの関数である。
それぞれ別の独立変数となっているので、この等式が成り立つためには、その値は定数で
なくてはならない。この定数を
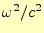 とする2。そうすると、
とする2。そうすると、
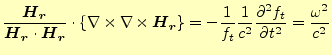 |
(15) |
である。2番目と3番目の式から、時間のみの微分方程式がつるられ、それはもはや偏微分
方程式ではなく、常微分方程式
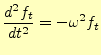 |
(16) |
になる。この微分方程式は、簡単に解けて
となる。ここで、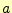 と
と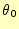 は初期条件により決まる定数である。これで、変数分
離した解(10)の時間の項が求まったわけである。この時間の項は、三
角関数になっている。
は初期条件により決まる定数である。これで、変数分
離した解(10)の時間の項が求まったわけである。この時間の項は、三
角関数になっている。
残りの空間の項
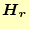 について、考えなくてならない。それが満たす偏微分
方程式を得るために、時間の項の結果である式(17)を、式
(12)に適用する。すると、
について、考えなくてならない。それが満たす偏微分
方程式を得るために、時間の項の結果である式(17)を、式
(12)に適用する。すると、
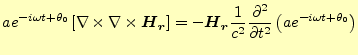 |
(18) |
となる。時間の項の微分を行うと、
となる。即ち時間の微分
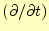 は、
は、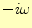 に置き換えられるので
ある。さらに整理すると、
に置き換えられるので
ある。さらに整理すると、
となる。これが、磁場の空間の偏微分連立方程式で、境界条件を課して解くことになる。
その解は磁場の空間分布を表す。これと、式(17)を掛けあわせた
ものが実際の電磁場の状態を表す。
この方程式の解は波になっており、電磁場は複素数で書かれるのが普通である。従って、
式(20)の
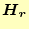 は複素数である。磁場を実数部
と虚数部
は複素数である。磁場を実数部
と虚数部
| |
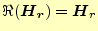 |
(21) |
| |
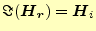 |
(22) |
とする。磁場の空間部分布を表す複素数
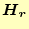 の
の
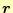 は太文字で、その
実数部である
は太文字で、その
実数部である
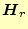 の
の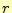 は通常の書体で記述しているので注意してほしい。これら
を使って、式(20)を実数部と虚数部を分けた方程式にすると、
は通常の書体で記述しているので注意してほしい。これら
を使って、式(20)を実数部と虚数部を分けた方程式にすると、
| |
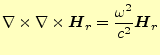 |
(23) |
| |
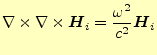 |
(24) |
となる。式(20)は、この2つの微分方程式を含んでいること
を忘れてはならない。
特に、進行波(Travelling Wave)を解析するときには、磁場は複素数になるので注意が必
要である。しかし、双方の方程式は同じではないか、と言う疑問が湧くかもしれない。微
分方程式は同じであるが境界条件が異なるから、実数部と虚数部の解は異なる。
定在波(Standing Wave)の場合は、実数部のみを考える。磁場は実数とするのである。
虚数部としても良いが、今までの慣習で実数部のみとする事になっている。
以上で、高周波電磁場の磁場が満たすべき方程式を示した。磁場と全く同じ方法で、電場
が表す方程式を計算できる。それは
となる。
電磁場分布を表す方程式は、磁場を表す式(20)と電場を表す
式(25)がある。それぞれは、独立ではなくマクスウェルの方
程式の式(3)や(4)で関連づけられている。
境界条件を考え計算しやすい方の場を求め、もう一方の場はマクスウェルの方程式に代入
(微分)することにより計算することになる。
ここでは、磁場の空間分布を示す式(20)の汎関数を示す。電場
についての式(25)も同じなので、読み替えてほしい。
式(20)の汎関数は
である。ここで、
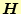 は磁場の空間分布である。式(20)で
は
は磁場の空間分布である。式(20)で
は
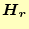 としていたが、簡潔に記述するために、添え字の
としていたが、簡潔に記述するために、添え字の
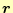 を省くこと
にする。また、アスタリスク
を省くこと
にする。また、アスタリスク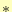 は複素共役(complex conjugate)を表す。このように
複素共役を使うと、汎関数が実数になり、ちょっとだけ計算が簡単になる。また、汎関数
はエネルギーに関係していることが多く、このようにすると磁場のエネルギーに関係した
量になるのである。わざわざ、複素共役を使わないで計算しても同じ結果が得られる。こ
の場合は、汎関数が複素数になる。
は複素共役(complex conjugate)を表す。このように
複素共役を使うと、汎関数が実数になり、ちょっとだけ計算が簡単になる。また、汎関数
はエネルギーに関係していることが多く、このようにすると磁場のエネルギーに関係した
量になるのである。わざわざ、複素共役を使わないで計算しても同じ結果が得られる。こ
の場合は、汎関数が複素数になる。
それでは、この式の第1 変分がゼロになる条件が式(20)を満足
するかどうか調べる。第一変分は、
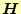 を
を
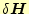 変化させたときの微小変化
量で
変化させたときの微小変化
量で
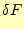 |
![$\displaystyle =F[\boldsymbol{H}+\delta\boldsymbol{H}]-F[\boldsymbol{H}]$](img64.png) |
|
| |
![$\displaystyle =\int\left[ \left\{\nabla\times\left(\boldsymbol{H}+\delta\boldsy...
...ght) \cdot \left(\boldsymbol{H}^\ast+\delta\boldsymbol{H}^\ast\right) \right]dV$](img65.png) |
|
| |
![$\displaystyle \qquad\qquad -\int\left[ \left(\nabla\times \boldsymbol{H}\right)...
...\left(\frac{\omega}{c}\right)^2\boldsymbol{H}\cdot\boldsymbol{H}^\ast\right ]dV$](img66.png) |
|
| |
2次の微少量を無視すると |
|
| |
![$\displaystyle =\int\left[ \left(\nabla\times \boldsymbol{H}\right)\cdot\left(\n...
...symbol{H}^\ast+ \boldsymbol{H}^\ast\cdot\delta\boldsymbol{H} \right\} \right]dV$](img67.png) |
|
| |
ベクトル恒等式
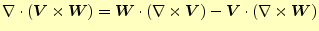 を 上 手につかう を 上 手につかう |
|
| |
 あるいは あるいは
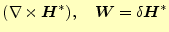 あるいは あるいは
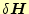 とする。 とする。 |
|
| |
![$\displaystyle =\int\left[ -\nabla\cdot\left\{(\nabla\times \boldsymbol{H})\time...
...rac{\omega}{c}\right)^2(\boldsymbol{H}\cdot\delta\boldsymbol{H}^\ast) \right]dV$](img72.png) |
|
| |
![$\displaystyle \qquad\qquad+\int\left[ -\nabla\cdot\left\{(\nabla\times \boldsym...
...rac{\omega}{c}\right)^2(\boldsymbol{H}^\ast\cdot\delta\boldsymbol{H}) \right]dV$](img73.png) |
|
| |
この式に発散定理を使い、式を整理すると |
|
| |
![$\displaystyle =-\int\left[ (\nabla\times \boldsymbol{H})\times\delta\boldsymbol...
...s \boldsymbol{H}^\ast )\times\delta\boldsymbol{H} \right]\cdot\boldsymbol{n}dS+$](img74.png) |
|
| |
![$\displaystyle \qquad\qquad \int\left[ \left\{\nabla\times\nabla\times\boldsymbo...
...ega}{c}\right)^2 \boldsymbol{H}^\ast\right\}\cdot\delta\boldsymbol{H} \right]dV$](img75.png) |
(27) |
となる。
いつものように、任意の
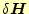 に対して、この第一変分
に対して、この第一変分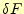 がゼロになる
条件を考える。しかし、今回は今までの「軸対称静電場の汎関数
」や「軸対称静磁場の汎関数
」と趣が異なり、関数が複素数になっている。第1変分
がゼロになる
条件を考える。しかし、今回は今までの「軸対称静電場の汎関数
」や「軸対称静磁場の汎関数
」と趣が異なり、関数が複素数になっている。第1変分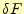 は実数であるが、
は実数であるが、
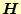 や
や
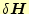 は複素数である。この複素数の実数部と虚数部の変化に対して、第1変分
がゼロとならなくてはならない。わかりやすくするために、複素数になっている部分を
は複素数である。この複素数の実数部と虚数部の変化に対して、第1変分
がゼロとならなくてはならない。わかりやすくするために、複素数になっている部分を
| |
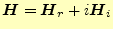 |
(28) |
| |
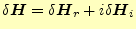 |
(29) |
と実数部と虚数部に分ける。これらを、式(27)に代入すると、
となる。これが、実数部と虚数部に分けた汎関数の第1変分である。もちろん、任意の
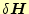 に対して、これがゼロになる条件を考えるのである。任意の
に対して、これがゼロになる条件を考えるのである。任意の
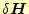 と言うことは、任意の
と言うことは、任意の
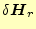 と
と
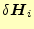 に対して、第
1変分がゼロになる条件を探すのである。
に対して、第
1変分がゼロになる条件を探すのである。
そのためには、この式の右辺第1項と2項がともにゼロにならなくてはならない。右辺第1
項は、境界条件を表し、
の場合、ゼロとなる。通常は、
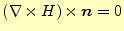 とする。これが自然境界条件
で、ノイマン条件となる。この磁場の回転は、式(4)より、
とする。これが自然境界条件
で、ノイマン条件となる。この磁場の回転は、式(4)より、
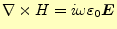 となる。従って、ノイマン条件は、
となる。従って、ノイマン条件は、
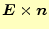 と書き直すことができる。すなわち、電場と境界の法線方向が一致
するのである。これは、金属の境界条件である。すなわち、境界を指定しなければ、自然
に金属の境界条件が満足されるのである。一方、
と書き直すことができる。すなわち、電場と境界の法線方向が一致
するのである。これは、金属の境界条件である。すなわち、境界を指定しなければ、自然
に金属の境界条件が満足されるのである。一方、
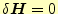 はディレクイ条件で、
境界の値を指定した場合である。
はディレクイ条件で、
境界の値を指定した場合である。
第2項がゼロとなるのは、
となる必要がある。これは、マクスウェルの方程式から導かれた磁場の偏微分方程式
(25)と全く同等である。
以上のことから、高周波の電磁場の磁場を計算するためには、式
(26)の第一変分をゼロにすればよいことが分かる。静磁場のマ
クスウェルの方程式は、式(26)の第1変分をゼロにするのと等
しいのである。
電場については、ここでは計算しないが、全く同じ手順で求められる。そして、結果も全
く同じである。
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年8月20日
![]() となる。
となる。
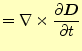
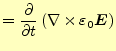
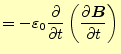
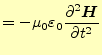
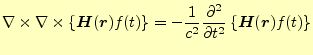
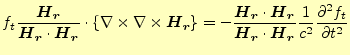
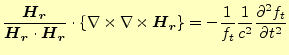
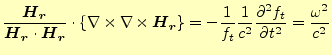
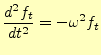
![]() について、考えなくてならない。それが満たす偏微分
方程式を得るために、時間の項の結果である式(17)を、式
(12)に適用する。すると、
について、考えなくてならない。それが満たす偏微分
方程式を得るために、時間の項の結果である式(17)を、式
(12)に適用する。すると、
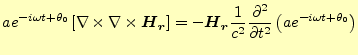
![]() は複素数である。磁場を実数部
と虚数部
は複素数である。磁場を実数部
と虚数部
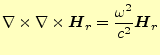
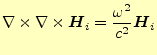
![]() を
を
![]() 変化させたときの微小変化
量で
変化させたときの微小変化
量で
![$\displaystyle =\int\left[ \left\{\nabla\times\left(\boldsymbol{H}+\delta\boldsy...
...ght) \cdot \left(\boldsymbol{H}^\ast+\delta\boldsymbol{H}^\ast\right) \right]dV$](img65.png)
![$\displaystyle \qquad\qquad -\int\left[ \left(\nabla\times \boldsymbol{H}\right)...
...\left(\frac{\omega}{c}\right)^2\boldsymbol{H}\cdot\boldsymbol{H}^\ast\right ]dV$](img66.png)
![$\displaystyle =\int\left[ \left(\nabla\times \boldsymbol{H}\right)\cdot\left(\n...
...symbol{H}^\ast+ \boldsymbol{H}^\ast\cdot\delta\boldsymbol{H} \right\} \right]dV$](img67.png)
![$\displaystyle =\int\left[ -\nabla\cdot\left\{(\nabla\times \boldsymbol{H})\time...
...rac{\omega}{c}\right)^2(\boldsymbol{H}\cdot\delta\boldsymbol{H}^\ast) \right]dV$](img72.png)
![$\displaystyle \qquad\qquad+\int\left[ -\nabla\cdot\left\{(\nabla\times \boldsym...
...rac{\omega}{c}\right)^2(\boldsymbol{H}^\ast\cdot\delta\boldsymbol{H}) \right]dV$](img73.png)
![$\displaystyle =-\int\left[ (\nabla\times \boldsymbol{H})\times\delta\boldsymbol...
...s \boldsymbol{H}^\ast )\times\delta\boldsymbol{H} \right]\cdot\boldsymbol{n}dS+$](img74.png)
![$\displaystyle \qquad\qquad \int\left[ \left\{\nabla\times\nabla\times\boldsymbo...
...ega}{c}\right)^2 \boldsymbol{H}^\ast\right\}\cdot\delta\boldsymbol{H} \right]dV$](img75.png)
![]() に対して、この第一変分
に対して、この第一変分![]() がゼロになる
条件を考える。しかし、今回は今までの「軸対称静電場の汎関数
」や「軸対称静磁場の汎関数
」と趣が異なり、関数が複素数になっている。第1変分
がゼロになる
条件を考える。しかし、今回は今までの「軸対称静電場の汎関数
」や「軸対称静磁場の汎関数
」と趣が異なり、関数が複素数になっている。第1変分![]() は実数であるが、
は実数であるが、
![]() や
や
![]() は複素数である。この複素数の実数部と虚数部の変化に対して、第1変分
がゼロとならなくてはならない。わかりやすくするために、複素数になっている部分を
は複素数である。この複素数の実数部と虚数部の変化に対して、第1変分
がゼロとならなくてはならない。わかりやすくするために、複素数になっている部分を
![$\displaystyle = -2\int\left[ (\nabla\times \boldsymbol{H}_r)\times\delta\boldsy...
...mes \boldsymbol{H}_i)\times\delta\boldsymbol{H}_i \right]\cdot\boldsymbol{n}dS+$](img84.png)
![$\displaystyle \qquad\qquad 2\int\left[ \left\{\nabla\times\nabla\times\boldsymb...
...mega}{c}\right)^2 \boldsymbol{H}_i\right\}\cdot\delta\boldsymbol{H}_i \right]dV$](img85.png)