[Previous: 3 高周波電磁場が満たす偏微分方程式] [Up: 軸対称高周波電磁場の汎関数] [Next: 5 軸対称進行波問題]
軸対称問題は、円柱座標系を使うのがセオリーである。この場合、空洞の形状は完全軸対 称である。定在波の場合、磁場は実数として取り扱うことができる。式 (26)では円柱座標系の回転の演算が表れ、それは
一般には、これを、汎関数の式(26)に代入することになる。し
かし、通常の空洞では最も共振周波数の低いモードが重要になる。図
1の加速空洞の場合、最低次のTMモードが運転に使われる。これが、
運転モードとなり、真っ先に解析したいモードである。このモードは、場が
![]() 方向の依存性を持たず、磁場は
方向の依存性を持たず、磁場は
![]() のみである。このモー
ドの磁場の回転は、
のみである。このモー
ドの磁場の回転は、
| (36) |
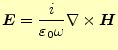 |
(37) |
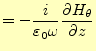 |
(38) | |
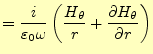 |
(39) |