[Previous: 3 静電場が満たす偏微分方程式] [Up: 軸対称電場の汎関数] [Next: 参考文献]
静電場の汎関数は式(9)で示したとおりである。この式 にはスカラーポテンシャルの勾配の演算が含まれる。円柱座標系の勾配は、以前示したとおり、
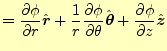 |
(14) |
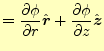 |
(15) |
この回転の結果を汎関数の式(9)に適用すると、
特に静電場の場合は、ラプラス方程式を計算することが多く、その場合は、式
(16)を![]() とすればよい。するの、その式は
静電場のエネルギーを表す式になる。その第一変分がゼロということは、安定状態はエネ
ルギーが停留値になることで、一般には最低エネルギーになる。エネルギーがもっとも小
さいときが安定なのである。
とすればよい。するの、その式は
静電場のエネルギーを表す式になる。その第一変分がゼロということは、安定状態はエネ
ルギーが停留値になることで、一般には最低エネルギーになる。エネルギーがもっとも小
さいときが安定なのである。