まずは、静電場が満たす方程式を示す。これはマクスウェルの方程式の時間の項をゼロとした式になる。それは、
と書き表せる。ここで、
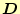 は電束密度、
は電束密度、
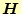 は電場の強さ、
は電場の強さ、
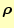 は電
荷密度を表す。ただし、物質中では
は電
荷密度を表す。ただし、物質中では
の関係がある。ここで、
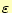 は誘電率である。これは、異方性の物質では2階の
テンソルとなる。しかし、ほとんど実用に使われている物質は、等方的である。そこで、
ここでは、等方的な物質のみを考えることにする。すると、それはスカラー量として取り
扱うことができ、計算が簡単になる。静電場の問題は、全て電束密度と電場の関係式
(3)を用い、連立偏微分方程式(1)と
(2)を解くことになる。これで、全てであるが、問題によっては簡
単に解けないのである。問題に応じた解法が必要となってくるが、基本はこれらの方程式
であることを忘れてはならない。
は誘電率である。これは、異方性の物質では2階の
テンソルとなる。しかし、ほとんど実用に使われている物質は、等方的である。そこで、
ここでは、等方的な物質のみを考えることにする。すると、それはスカラー量として取り
扱うことができ、計算が簡単になる。静電場の問題は、全て電束密度と電場の関係式
(3)を用い、連立偏微分方程式(1)と
(2)を解くことになる。これで、全てであるが、問題によっては簡
単に解けないのである。問題に応じた解法が必要となってくるが、基本はこれらの方程式
であることを忘れてはならない。
通常、静電場の問題では電場
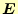 を計算するより、ポテンシャルを計算する方が簡単
である。電場はベクトルで未知数が3個あるが、ポテンシャルはスカラーなので未知数が1
個で済む。どう見ても計算が簡単である。このポテンシャル
を計算するより、ポテンシャルを計算する方が簡単
である。電場はベクトルで未知数が3個あるが、ポテンシャルはスカラーなので未知数が1
個で済む。どう見ても計算が簡単である。このポテンシャル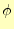 は、正確にはスカラーポテン
シャルと言い
は、正確にはスカラーポテン
シャルと言い
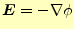 |
(4) |
と定義される。こうすることにより、静電場のマクスウェルの方程式
(2)が自動的に満足される2。
これで、静電場のマクスウェルの方程式のひとつが満足したので、残りを満足させるため
のスカラーポテンシャルの条件を探せばよい。残りの式(1)と式
(3)、そしてスカラーポテンシャルの定義とから、
が直ちに分かる。これが静電場を計算するときのスカラーポテンシャルが満たすべき偏微
分方程式である。右辺と左辺を入れ替えて、見栄えよく記述すると
となる。以前求めた、静磁場のベクトルポテンシャルが満足す
る偏微分方程式と似た形をしている。次節では、この汎関数を示す。
汎関数を示す前に、もう少し一般的なことを述べておく。誘電率は一定と考えることが多
い。その場合、誘電率は積分の外に出すことができ、
となる。これは、ポアッソン(Poisson)方程式と呼ばれる。また、計算する領域内に電荷
が無い問題も多く、その場合は
となる。これは、ラプラス(Laplace)方程式と呼ばれる。
実際の静電場の問題では、マクスウェルの方程式から直接導かれる式
(1)や(2)の代わりに、適当な境界条件を
課して、式(6)や(7)、
(8)を計算することにある。これらの式のうち、条件に適合した最も
簡単式を選択するのは言うまでもない。次節ではもっとも条件の厳しい、式
(6)の汎関数を示す。
静磁場の汎関数から、静電場のそれは
と想像できる。本当かどうか、この式の第一変分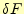 を計算し、それがゼロになる条件を
考えることにする。第一変分は、
を計算し、それがゼロになる条件を
考えることにする。第一変分は、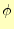 を
を
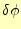 変化させたときの微小変化量で
変化させたときの微小変化量で
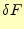 |
![$\displaystyle =F[\phi+\delta\phi]-F[\phi]$](img25.png) |
|
| |
![$\displaystyle =\int\left[\frac{\varepsilon}{2} \left\{\nabla\left(\phi+\delta\p...
...\phi+\delta\phi\right)\right\} -\rho\cdot\left(\phi+\delta\phi\right) \right]dV$](img26.png) |
|
| |
![$\displaystyle \qquad\qquad -\int\left[\frac{\varepsilon}{2} \left(\nabla\phi\right)^2 -\rho\phi \right]dV$](img27.png) |
|
| |
![$\displaystyle =\int\left[\frac{\varepsilon}{2} \left\{\left(\nabla \phi \right)...
...) +\left(\nabla \delta\phi \right)^2\right\} -\rho\phi-\rho\delta\phi \right]dV$](img28.png) |
|
| |
![$\displaystyle \qquad\qquad -\int\left[\frac{\varepsilon}{2} \left(\nabla\phi\right)^2 -\rho\phi \right]dV$](img29.png) |
|
| |
2次の微少量を無視すると |
|
| |
![$\displaystyle =\int\left[\varepsilon \left(\nabla \phi \right)\cdot\left(\nabla \delta\phi \right) -\rho\delta\phi \right]dV \nonumber$](img30.png) |
|
| |
ベクトル恒等式
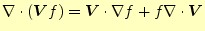 を 上 手につかう を 上 手につかう |
|
| |
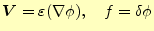 とする。 とする。 |
|
| |
![$\displaystyle =\int\left[ \nabla\cdot\left\{\varepsilon(\nabla \phi )\delta\phi...
...\phi\nabla\cdot\left\{\varepsilon(\nabla\phi)\right\} -\rho\delta\phi \right]dV$](img33.png) |
|
| |
この式の第1項に発散定理を使い、式を整理すると |
|
| |
![$\displaystyle =\int\varepsilon(\nabla \phi )\delta\phi\cdot\boldsymbol{n}dS+ \int\left[ \nabla\cdot(\varepsilon\nabla\phi)-\rho \right]\delta\phi dV$](img34.png) |
(10) |
となる。
いつものように、任意の
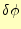 に対して、この第一変分
に対して、この第一変分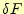 がゼ
ロになる条件を考える。そのためには、式(10)の右辺の第1項と
第2項の被積分関数がともにゼロになる必要がある。まず、第1項であるが、それは
がゼ
ロになる条件を考える。そのためには、式(10)の右辺の第1項と
第2項の被積分関数がともにゼロになる必要がある。まず、第1項であるが、それは
| |
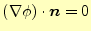 |
(11) |
| |
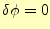 |
(12) |
のいずれかである。最初の条件はノイマン条件で、何も境界条件を指定しなければ、電場
と境界は平行になると言うことであ。2番目のものは、境界でのスカラーポテンシャルを指定するディレ
クレ条件である。即ち、第一変分の右辺第1項は境界条件を表すのである。
次に、第2項であるが、これは計算している領域で
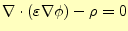 |
(13) |
となる必要がある。これは、スカラーポテンシャルを用いた静電場のマクスウェルの方程
式そのもので、式(6)と等しい。
以上のことから、静電場を計算するためには、式(9)の
第一変分をゼロにすればよいことが分かる。静電場のマクスウェルの方程式は、式
(9)の第1変分をゼロにするのと等しいのである。
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年8月20日
![]() を計算するより、ポテンシャルを計算する方が簡単
である。電場はベクトルで未知数が3個あるが、ポテンシャルはスカラーなので未知数が1
個で済む。どう見ても計算が簡単である。このポテンシャル
を計算するより、ポテンシャルを計算する方が簡単
である。電場はベクトルで未知数が3個あるが、ポテンシャルはスカラーなので未知数が1
個で済む。どう見ても計算が簡単である。このポテンシャル![]() は、正確にはスカラーポテン
シャルと言い
は、正確にはスカラーポテン
シャルと言い
![$\displaystyle =\int\left[\frac{\varepsilon}{2} \left\{\nabla\left(\phi+\delta\p...
...\phi+\delta\phi\right)\right\} -\rho\cdot\left(\phi+\delta\phi\right) \right]dV$](img26.png)
![$\displaystyle \qquad\qquad -\int\left[\frac{\varepsilon}{2} \left(\nabla\phi\right)^2 -\rho\phi \right]dV$](img27.png)
![$\displaystyle =\int\left[\frac{\varepsilon}{2} \left\{\left(\nabla \phi \right)...
...) +\left(\nabla \delta\phi \right)^2\right\} -\rho\phi-\rho\delta\phi \right]dV$](img28.png)
![$\displaystyle \qquad\qquad -\int\left[\frac{\varepsilon}{2} \left(\nabla\phi\right)^2 -\rho\phi \right]dV$](img29.png)
![$\displaystyle =\int\left[\varepsilon \left(\nabla \phi \right)\cdot\left(\nabla \delta\phi \right) -\rho\delta\phi \right]dV \nonumber$](img30.png)
![$\displaystyle =\int\left[ \nabla\cdot\left\{\varepsilon(\nabla \phi )\delta\phi...
...\phi\nabla\cdot\left\{\varepsilon(\nabla\phi)\right\} -\rho\delta\phi \right]dV$](img33.png)
![$\displaystyle =\int\varepsilon(\nabla \phi )\delta\phi\cdot\boldsymbol{n}dS+ \int\left[ \nabla\cdot(\varepsilon\nabla\phi)-\rho \right]\delta\phi dV$](img34.png)
![]() に対して、この第一変分
に対して、この第一変分![]() がゼ
ロになる条件を考える。そのためには、式(10)の右辺の第1項と
第2項の被積分関数がともにゼロになる必要がある。まず、第1項であるが、それは
がゼ
ロになる条件を考える。そのためには、式(10)の右辺の第1項と
第2項の被積分関数がともにゼロになる必要がある。まず、第1項であるが、それは