まずは、電磁石の磁場が満たす方程式を示す。これは静磁場のマクスウェルの方程式で、
その時間の項をゼロとした式になる。それは、
と書き表せる。ここで、
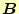 は磁束密度、
は磁束密度、
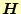 は磁場の強さ、
は磁場の強さ、
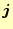 は電流密度を表
す。ただし、物質中では
は電流密度を表
す。ただし、物質中では
の関係がある。ここで、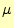 は透磁率である。これは、異方性の物質では2階のテンソル
となる。しかし、ほとんど実用に使われている物質は、等方的である。そこで、ここでは、
等方的な物質のみを考えることにする。すると、それはスカラー量として取り扱うことが
でき、計算が簡単になる。
は透磁率である。これは、異方性の物質では2階のテンソル
となる。しかし、ほとんど実用に使われている物質は、等方的である。そこで、ここでは、
等方的な物質のみを考えることにする。すると、それはスカラー量として取り扱うことが
でき、計算が簡単になる。
ここで解析しようとする軸対称問題では、ベクトルポテンシャルを使う方が、後で示すよ
うに、式が簡単になる。ベクトルポテンシャル
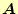 の定義は、
の定義は、
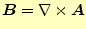 |
(4) |
である。これと式(3)から、直ちに
 |
(5) |
が分かる。この式の両辺に回転の演算を施し、式(2)を使うと
が得られる。これが、ベクトルポテンシャルが満たす偏微分方程式である。実際の磁場は、
このベクトルポテンシャルを計算して、微分(回転)することにより得られる。
いろいろな教科書に書かれているように、式(6)の汎関数は
である。本当かどうか、この式の第一変分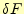 を計算し、それがゼロになる条件を
考えることにする。第一変分は、
を計算し、それがゼロになる条件を
考えることにする。第一変分は、
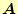 を
を
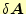 変化させたときの微小変化量で
変化させたときの微小変化量で
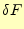 |
![$\displaystyle =F[\boldsymbol{A}+\delta\boldsymbol{A}]-F[\boldsymbol{A}]$](img18.png) |
|
| |
![$\displaystyle =\int\left[\frac{1}{2\mu} \left\{\nabla\times\left(\boldsymbol{A}...
... -\boldsymbol{j}\cdot\left(\boldsymbol{A}+\delta\boldsymbol{A}\right) \right]dV$](img19.png) |
|
| |
![$\displaystyle \qquad\qquad -\int\left[\frac{1}{2\mu} \left(\nabla\times\boldsymbol{A}\right)^2 -\boldsymbol{j}\cdot\boldsymbol{A} \right]dV$](img20.png) |
|
| |
![$\displaystyle =\int\left[\frac{1}{2\mu} \left\{\left(\nabla\times \boldsymbol{A...
... -\boldsymbol{j}\cdot\left(\boldsymbol{A}+\delta\boldsymbol{A}\right) \right]dV$](img21.png) |
|
| |
![$\displaystyle \qquad\qquad -\int\left[\frac{1}{2\mu} \left(\nabla\times\boldsymbol{A}\right)^2 -\boldsymbol{j}\cdot\boldsymbol{A} \right]dV$](img22.png) |
|
| |
2次の微少量を無視すると |
|
| |
![$\displaystyle =\int\left[\frac{1}{\mu} \left(\nabla\times \boldsymbol{A}\right)...
...symbol{A}\right) -(\delta\boldsymbol{A}\cdot\boldsymbol{j}) \right]dV \nonumber$](img23.png) |
|
| |
ベクトル恒等式
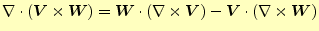 を 上 手につかう を 上 手につかう |
|
| |
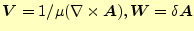 とする。 とする。 |
|
| |
![$\displaystyle =\int\left[ -\nabla\cdot\left\{\frac{1}{\mu}(\nabla\times \boldsy...
...mes\boldsymbol{A})\right\} -(\delta\boldsymbol{A}\cdot\boldsymbol{j}) \right]dV$](img26.png) |
|
| |
この式の第1項に発散定理を使い、式を整理すると |
|
| |
![$\displaystyle =-\int\frac{1}{\mu}(\nabla\times \boldsymbol{A})\times\delta\bold...
...times\boldsymbol{A}) -\boldsymbol{j}\right\}\cdot\delta\boldsymbol{A} \right]dV$](img27.png) |
(8) |
となる。
いつものように、任意の
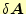 に対して、この第一変分
に対して、この第一変分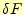 がゼ
ロになる条件を考える。そのためには、式(8)の右辺の第1項と
第2項の被積分関数がともにゼロになる必要がある。まず、第1項であるが、それは
がゼ
ロになる条件を考える。そのためには、式(8)の右辺の第1項と
第2項の被積分関数がともにゼロになる必要がある。まず、第1項であるが、それは
| |
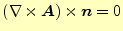 |
(9) |
| |
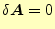 |
(10) |
のいずれかである2。最初の条件はノイマン条件で、何も境界条件を指定しなければ、磁場
は境界と垂直になる。2番目のものは、境界でのベクトルポテンシャルを指定するディレ
クレ条件である。即ち、第一変分の右辺第1項は境界条件を表すのである。
次に、第2項であるが、これは計算している領域で
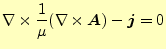 |
(11) |
となる必要がある。これは、ベクトルポテンシャルを用いた静磁場のマクスウェルの方程
式そのもので、式(6)と等しい。
以上のことから、静磁場を計算するためには、式(7)の
第一変分をゼロにすればよいことが分かる。静磁場のマクスウェルの方程式は、式
(7)の第1変分をゼロにするのと等しいのである。
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成19年8月20日
![]() の定義は、
の定義は、
![$\displaystyle =\int\left[\frac{1}{2\mu} \left\{\nabla\times\left(\boldsymbol{A}...
... -\boldsymbol{j}\cdot\left(\boldsymbol{A}+\delta\boldsymbol{A}\right) \right]dV$](img19.png)
![$\displaystyle \qquad\qquad -\int\left[\frac{1}{2\mu} \left(\nabla\times\boldsymbol{A}\right)^2 -\boldsymbol{j}\cdot\boldsymbol{A} \right]dV$](img20.png)
![$\displaystyle =\int\left[\frac{1}{2\mu} \left\{\left(\nabla\times \boldsymbol{A...
... -\boldsymbol{j}\cdot\left(\boldsymbol{A}+\delta\boldsymbol{A}\right) \right]dV$](img21.png)
![$\displaystyle \qquad\qquad -\int\left[\frac{1}{2\mu} \left(\nabla\times\boldsymbol{A}\right)^2 -\boldsymbol{j}\cdot\boldsymbol{A} \right]dV$](img22.png)
![$\displaystyle =\int\left[\frac{1}{\mu} \left(\nabla\times \boldsymbol{A}\right)...
...symbol{A}\right) -(\delta\boldsymbol{A}\cdot\boldsymbol{j}) \right]dV \nonumber$](img23.png)
![$\displaystyle =\int\left[ -\nabla\cdot\left\{\frac{1}{\mu}(\nabla\times \boldsy...
...mes\boldsymbol{A})\right\} -(\delta\boldsymbol{A}\cdot\boldsymbol{j}) \right]dV$](img26.png)
![$\displaystyle =-\int\frac{1}{\mu}(\nabla\times \boldsymbol{A})\times\delta\bold...
...times\boldsymbol{A}) -\boldsymbol{j}\right\}\cdot\delta\boldsymbol{A} \right]dV$](img27.png)
![]() に対して、この第一変分
に対して、この第一変分![]() がゼ
ロになる条件を考える。そのためには、式(8)の右辺の第1項と
第2項の被積分関数がともにゼロになる必要がある。まず、第1項であるが、それは
がゼ
ロになる条件を考える。そのためには、式(8)の右辺の第1項と
第2項の被積分関数がともにゼロになる必要がある。まず、第1項であるが、それは