ラプラス方程式は物理学の分野ではよく出て来る式である。
3変数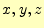 の関数
の関数
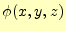 の場合
の場合
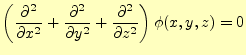 |
(1) |
をいう。これを
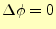 と書くことも多い。
この方程式に従う関数の例は、静電場、重力ポテンシャル、定常状態の温度分布
等がある。
と書くことも多い。
この方程式に従う関数の例は、静電場、重力ポテンシャル、定常状態の温度分布
等がある。
今は、2次元の場合のラプラス方程式を考える。2次元のラプラス方程式は以下のようになる。
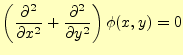 |
(2) |
有限要素法ではこの微分方程式を変分形の方程式に直して計算していく。
次に示すラプラス方程式の変分形を、有限要素法で解く方法を導出する。
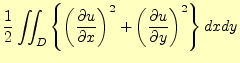 |
(3) |
領域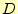 の中で、ラプラス方程式を解くときに、まず領域を三角形要素に分割する。
要素には番号がふられているものとして、
の中で、ラプラス方程式を解くときに、まず領域を三角形要素に分割する。
要素には番号がふられているものとして、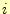 番目の要素の領域は、
(便宜上)
番目の要素の領域は、
(便宜上)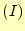 と表すものとする。
このときの、三角形の頂点にあたる節点の値を求めようとする。
この節点には番号がふられているものとし、節点
と表すものとする。
このときの、三角形の頂点にあたる節点の値を求めようとする。
この節点には番号がふられているものとし、節点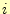 の
の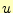 の値を
の値を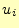 とする。
節点での
とする。
節点での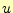 の値
の値
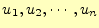 をすべて計算することにより、
領域全体にわたり
をすべて計算することにより、
領域全体にわたり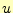 の値を近似していく。
の値を近似していく。
未知関数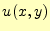 を近似するために、次のような一次関数の形状関数を導入する。
要素
を近似するために、次のような一次関数の形状関数を導入する。
要素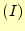 の頂点が、節点
の頂点が、節点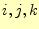 だったとするとき、形状関数
だったとするとき、形状関数
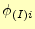 は、
は、
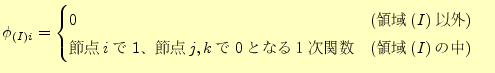 |
(4) |
のようになり、具体的な
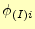 を表すと、以下のようになる。
を表すと、以下のようになる。
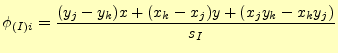 |
(5) |
ここで、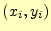 は節点
は節点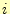 の座標、
の座標、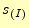 は領域
は領域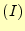 の面積である。
の面積である。
一つの領域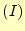 の中の求める方程式は、次の形で近似される。
の中の求める方程式は、次の形で近似される。
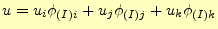 |
(6) |
解くべき領域全体では、この方程式の足し合わせで近似される。
領域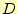 全体では以下のようになる。
全体では以下のようになる。
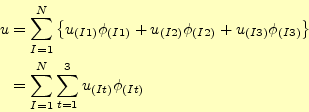 |
(7) |
この式の添え字の説明をする。
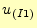 の意味は、要素番号
の意味は、要素番号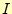 の三角形領域が持っている一つ目の節点での、
の三角形領域が持っている一つ目の節点での、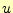 の値。
同様に、
の値。
同様に、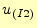 は、要素番号
は、要素番号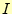 の三角形領域が持っている二つ目の節点での、
の三角形領域が持っている二つ目の節点での、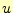 の値。
また、
の値。
また、
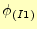 の意味は、要素番号
の意味は、要素番号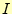 の三角形領域が持っている一つ目の節点が
節点
の三角形領域が持っている一つ目の節点が
節点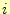 だったとすると、
だったとすると、
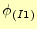 は
は
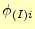 と等価である。
と等価である。
このような形状関数を使い、![$ J[u]$](img42.png) の変分を計算していく。
の変分を計算していく。
汎関数![$ J[u]$](img43.png) を決定関数を使って表すと、次のようになる。
を決定関数を使って表すと、次のようになる。
![\begin{displaymath}\begin{split} J[u] &= \frac{1}{2}\int\!\!\!\int_D\left\{\lef...
...tial \phi_{(It)}}{\partial y}\right)^2\right\}dxdy \end{split}\end{displaymath}](img44.png) |
(8) |
汎関数![$ J[u]$](img45.png) が、関数
が、関数
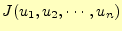 になったので、
になったので、
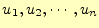 で偏微分していく。
ただし、
で偏微分していく。
ただし、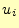 が固定点(ディレクレ条件)だった場合は除く。
が固定点(ディレクレ条件)だった場合は除く。
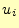 で偏微分した場合を計算していく。
この場合、変数として
で偏微分した場合を計算していく。
この場合、変数として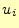 を含む積分領域だけ抜き出して計算すればよい。
すなわち、以下のようになる。
を含む積分領域だけ抜き出して計算すればよい。
すなわち、以下のようになる。
![\begin{displaymath}\begin{split} \frac{\partial J[u]}{\partial u_i} &= \frac{...
...}}{\partial y}\right)^2\right\}dxdy \\ &+ \cdots \end{split}\end{displaymath}](img51.png) |
(9) |
ここでの、領域
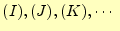 は頂点に節点
は頂点に節点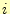 をもつ三角形領域である。
つまり、節点
をもつ三角形領域である。
つまり、節点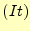 のどれか(節点
のどれか(節点
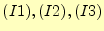 のどれか)は節点
のどれか)は節点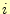 である
(節点
である
(節点 も同様)。
も同様)。
さらに計算していくと以下のようになる。
![\begin{displaymath}\begin{split} \frac{\partial J[u]}{\partial u_i} &= \frac{...
...}}{\partial y}\right)^2\right\}dxdy \\ &+ \cdots \end{split}\end{displaymath}](img58.png) |
(10) |
ここで、
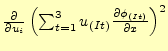 を計算すると、以下のようになる。
を計算すると、以下のようになる。
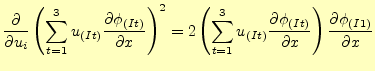 |
(11) |
ここで、
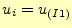 であるとしている。
であるとしている。
これをもとに、
![\begin{displaymath}\begin{split} \frac{\partial J[u]}{\partial u_i} &= \int\!...
...i_{(K)i}}{\partial y} \right\}dxdy \\ &+ \cdots \end{split}\end{displaymath}](img62.png) |
(12) |
となる。ここで、
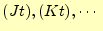 のそれぞれにおいて、
3つのうちどれかは節点
のそれぞれにおいて、
3つのうちどれかは節点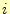 を示すものである。
さらに、積分の中には、変数として
を示すものである。
さらに、積分の中には、変数として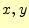 が入っていないので、以下のようになる。
が入っていないので、以下のようになる。
![\begin{displaymath}\begin{split} \frac{\partial J[u]}{\partial u_i} &= \left\...
... \right\} \int\!\!\!\int_{(K)} dxdy \\ &+ \cdots \end{split}\end{displaymath}](img66.png) |
(13) |
ここで、積分
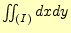 はその領域の面積である。
これを
はその領域の面積である。
これを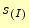 とすると、
とすると、
![\begin{displaymath}\begin{split} \frac{\partial J[u]}{\partial u_i} &= \left\...
...(K)i}}{\partial y} \right\} s_{(K)} \\ &+ \cdots \end{split}\end{displaymath}](img69.png) |
(14) |
となる。
連立方程式は、
![$ \frac{\partial J[u]}{\partial u_i}=0$](img70.png) としたものを連立させる。
また、ディレクレ条件の場合はその点での値がわかっているので、
としたものを連立させる。
また、ディレクレ条件の場合はその点での値がわかっているので、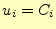 とする。
とする。
![\begin{displaymath}\begin{cases} \frac{\partial J[u]}{\partial u_1} = 0 \\ \f...
... u_{m+1} = C_{m+1} \\ \ \ \vdots \\ u_n = C_n \end{cases}\end{displaymath}](img72.png) |
(15) |
ここで、ディレクレ条件ではない節点を、節点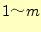 として、
ディレクレ条件の節点を、節点
として、
ディレクレ条件の節点を、節点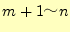 としている。
これを行列
としている。
これを行列
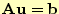 の形で表すと、
の形で表すと、
 |
(16) |
これより、
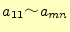 までを求めなくてはいけないことが分かる。
までを求めなくてはいけないことが分かる。
ホームページ: Yamamoto's laboratory
著者: 夏井拓也
Yamamoto Masashi
平成19年8月20日
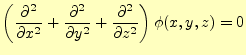
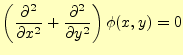
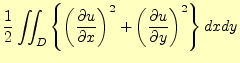
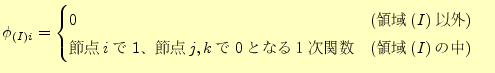
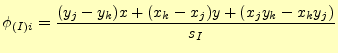
![]() の中の求める方程式は、次の形で近似される。
の中の求める方程式は、次の形で近似される。
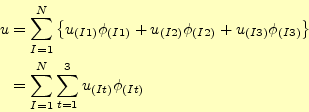
![]() の変分を計算していく。
の変分を計算していく。
![\begin{displaymath}\begin{split} J[u] &= \frac{1}{2}\int\!\!\!\int_D\left\{\lef...
...tial \phi_{(It)}}{\partial y}\right)^2\right\}dxdy \end{split}\end{displaymath}](img44.png)
![]() で偏微分した場合を計算していく。
この場合、変数として
で偏微分した場合を計算していく。
この場合、変数として![]() を含む積分領域だけ抜き出して計算すればよい。
すなわち、以下のようになる。
を含む積分領域だけ抜き出して計算すればよい。
すなわち、以下のようになる。
![\begin{displaymath}\begin{split} \frac{\partial J[u]}{\partial u_i} &= \frac{...
...}}{\partial y}\right)^2\right\}dxdy \\ &+ \cdots \end{split}\end{displaymath}](img51.png)
![\begin{displaymath}\begin{split} \frac{\partial J[u]}{\partial u_i} &= \frac{...
...}}{\partial y}\right)^2\right\}dxdy \\ &+ \cdots \end{split}\end{displaymath}](img58.png)
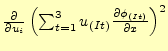 を計算すると、以下のようになる。
を計算すると、以下のようになる。
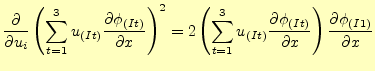
![\begin{displaymath}\begin{split} \frac{\partial J[u]}{\partial u_i} &= \int\!...
...i_{(K)i}}{\partial y} \right\}dxdy \\ &+ \cdots \end{split}\end{displaymath}](img62.png)
![\begin{displaymath}\begin{split} \frac{\partial J[u]}{\partial u_i} &= \left\...
... \right\} \int\!\!\!\int_{(K)} dxdy \\ &+ \cdots \end{split}\end{displaymath}](img66.png)
![\begin{displaymath}\begin{cases} \frac{\partial J[u]}{\partial u_1} = 0 \\ \f...
... u_{m+1} = C_{m+1} \\ \ \ \vdots \\ u_n = C_n \end{cases}\end{displaymath}](img72.png)
