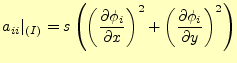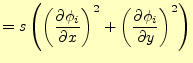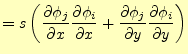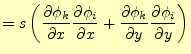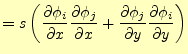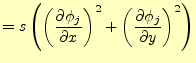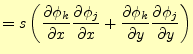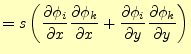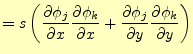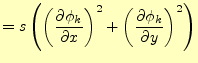前章のように、連立方程式を一本づつ計算していくと、節点のまわりに
どの要素があるか、という情報が必要になり、あまり効率的ではない。
1
ここでは、要素と節点の関係が分かっているとする。
式(14)の各項は、要素一つの寄与である。
ここで、式(14)から要素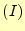 の寄与だけを抜き出す。
の寄与だけを抜き出す。
![$\displaystyle \left. \frac{\partial J[u]}{\partial u_i} \right\vert _{(I)} = ...
...}}{\partial y}\right) \frac{\partial \phi_{(I)i}}{\partial y} \right\} s_{(I)}$](img79.png) |
(17) |
この式での、節点
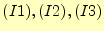 を本来の節点番号
を本来の節点番号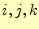 と置き、
要素番号は
と置き、
要素番号は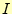 しか出てこないので、これは省略すると次のようになる。
しか出てこないので、これは省略すると次のようになる。
![\begin{displaymath}\begin{split} \left. \frac{\partial J[u]}{\partial u_i} \rig...
... y} \frac{\partial \phi_i}{\partial y} \right) u_k \end{split}\end{displaymath}](img83.png) |
(18) |
これを参考に
![$ \frac{\partial J[u]}{\partial u_j}$](img84.png) の
要素
の
要素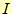 の寄与分を考えると次のようになる。
の寄与分を考えると次のようになる。
![$\displaystyle \left. \frac{\partial J[u]}{\partial u_j} \right\vert _{(I)} = s...
...rac{\partial \phi_k}{\partial y} \frac{\partial \phi_j}{\partial y} \right) u_k$](img86.png) |
(19) |
同様に
![$ \frac{\partial J[u]}{\partial u_k}$](img87.png) の
要素
の
要素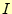 の寄与分を考えると次のようになる。
の寄与分を考えると次のようになる。
![$\displaystyle \left. \frac{\partial J[u]}{\partial u_k} \right\vert _{(I)} = s...
...} \right)^2 + \left( \frac{\partial \phi_k}{\partial y} \right)^2 \right) u_k$](img89.png) |
(20) |
このように、一つの要素の方程式の寄与(式の中の項)をすべての要素について求め、
それをすべて足しあわせると解くべき連立方程式ができる。
式(18),(19),(20)の結果を係数行列に直す。
![$ \frac{\partial J[u]}{\partial u_i}$](img90.png) は、
は、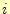 行。その中の、
行。その中の、
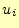 を含む項は、
を含む項は、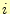 列になるので、
列になるので、
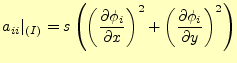 |
(21) |
となり、後は同様にして求められる。
この中に入っている形状関数は、もちろん今考えている要素の中にある形状関数である。
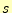 も今考えている要素の面積である。
も今考えている要素の面積である。
このように、すべての要素の係数行列の寄与分を考えて、足しあわせると解くべき方程式の
係数行列ができる。このような方法で係数行列を決めていく方法は実際に
プログラムを組む上で非常に楽である。
ホームページ: Yamamoto's laboratory
著者: 夏井拓也
Yamamoto Masashi
平成19年8月20日
![$\displaystyle \left. \frac{\partial J[u]}{\partial u_i} \right\vert _{(I)} = ...
...}}{\partial y}\right) \frac{\partial \phi_{(I)i}}{\partial y} \right\} s_{(I)}$](img79.png)
![]() は、
は、![]() 行。その中の、
行。その中の、
![]() を含む項は、
を含む項は、![]() 列になるので、
列になるので、