


: トリプレットのシミュレーション
: Q-magnetのシミュレーション
: Q-magnetのシミュレーション
今、それぞれ10mmの幅を持ったmagnetを40mm離したダブレットがあるとする。
このダブレットを使い、1MeVの平行ビームをmagnetから200mmの位置で収束させる条件を考えてみる。
まず、式(7), (10)より、
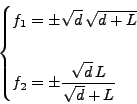 |
(16) |
なので、
である。また、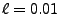 であるので、
であるので、
となり、
と求められる。
この結果を、GPTを使ってシミュレーションしてみる。
まず、以下のようなGPTのインプットファイルを用意する。
# Define beam parameters
gamma = 1/0.511 +1 ;
radius= 6e-3 ;
# Start initial beam
setparticles("beam",100,me,qe,0.0) ;
setrxydist("beam","u",radius/2, radius) ;
setphidist("beam","u",0,2*pi) ;
setGdist("beam","u",gamma,0) ;
# Position the quadrupole lenses
quadrupole( "wcs","z",0.1, 0.01, 4.84099 ) ;
quadrupole( "wcs","z",0.14, 0.01, -5.80919 ) ;
# Specify output times
tout(0,4e-9,0.01e-9) ;
このファイルは、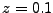 [m]と
[m]と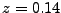 [m]のところにQ-magnetを置くように指定している。
このファイルをGPTで走らせた結果は、図1, 2のようになった。
ほぼ計算道理になっているが、若干ずれがある。
これはthin-lens近似によるものだと思う。
[m]のところにQ-magnetを置くように指定している。
このファイルをGPTで走らせた結果は、図1, 2のようになった。
ほぼ計算道理になっているが、若干ずれがある。
これはthin-lens近似によるものだと思う。
natsui takuya
平成19年2月9日
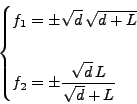
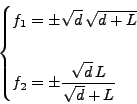
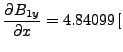 T/m
T/m![$\displaystyle ] \, , \, \, \frac{\partial B_{2y}}{\partial x} = -5.80919 \,[$](img35.png) T/m
T/m