[Previous: 1 はじめに] [Up: 2次要素と2次曲線要素を使った有限要素法のための計算] [Next: 3 曲線要素]
2次要素の場合、まず1次要素と同じに頂点に節点を3つ持ち、そのほかに辺の 真ん中に3つ節点を持つ。つまり、図1のように節点を持ってい ることになる。 また、座標変換したときの三角形要素を図2に示す。
この変換の式は以下のようになる。
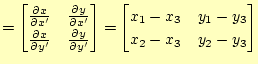 |
(5) | |
| (6) |
| (7) |
ここで、![]() を具体的に決めなければならないが、これは2次関数で、節点
を具体的に決めなければならないが、これは2次関数で、節点![]() では
では![]() 、それ以外の節点では
、それ以外の節点では![]() となることを考えると簡単に決まる。
とくに座標変換した座標系で考えると楽である。
形状関数は以下のようになる。
となることを考えると簡単に決まる。
とくに座標変換した座標系で考えると楽である。
形状関数は以下のようになる。
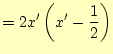 |
(8) | |
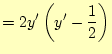 |
(9) | |
 |
(10) | |
| (11) | ||
| (12) | ||
| (13) |
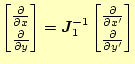 |
(14) |
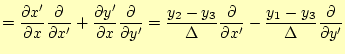 |
(15) | |
 |
(16) |
| (17) | ||
| (18) | ||
| (19) | ||
| (20) | ||
| (21) | ||
| (22) | ||
| (23) | ||
| (24) | ||
| (25) | ||
| (26) | ||
| (27) | ||
| (28) |