[Previous: 2 直線要素] [Up: 2次要素と2次曲線要素を使った有限要素法のための計算] [Next: この文書について...]
この曲線は、![]() の形の2次関数を移動(回転と平行移動)させたもので、
節点4の位置での傾きが、節点1と節点2を通る直線の傾きに等しいとする。
の形の2次関数を移動(回転と平行移動)させたもので、
節点4の位置での傾きが、節点1と節点2を通る直線の傾きに等しいとする。
まずは、直線の三角形要素を座標変換したときと同じ式で座標変換する。 その図を図4に示す。
この変換の式は直線要素を変換した式に等しい。つまり、
式(1),(2)で表される。
また、図4の中の、![]() は
は![]() 座標での節点4の座標
である。その意味では、
座標での節点4の座標
である。その意味では、
![]() と表した方がよかったかも。
これを求めると以下のようになる。
と表した方がよかったかも。
これを求めると以下のようになる。
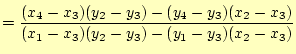 |
(29) | |
 |
(30) |
曲線要素を座標変換するときは、その変換が二段階に分かれていて、
![]() と変換していく。
と変換していく。
さあいよいよ曲線を直線に変える。この変換は線形ではない、と思う。 とりあえずその式は、以下のようになる。
| (31) | ||
| (32) |
次に、![]() を
を![]() を使って表してみると、以下のようになる。
を使って表してみると、以下のようになる。
 |
(35) | |
| (36) |
また演算子の変換は、
 |
(37) |
 |
(40) | |
 |
(41) | |
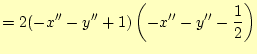 |
(42) | |
| (43) | ||
| (44) | ||
| (45) |
でも、ここで書くのは面倒なので、省略。