2 ラグランジュ補間
2.1 基本的な考え方
ある物理量を測定してと補間するわけです。この係数
連立方程式の計算は時間がかかります。それに代わるもっと良い方法がありま す。ここではN次関数で表現できれば良いわけで、以下がそれになります。
この式(2)を見ると、
- 各項の分子は定数である。分母はN次関数です。このことから、全て の項はN次関数になっているので、この式はN次関数(N次多項式)です。
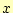 に
に
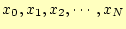 を代入すると、
を代入すると、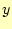 の値は
の値は
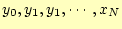 になることが分かります。これは、データ点
になることが分かります。これは、データ点
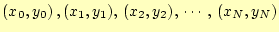 の全てを
通過していることを示してます。
の全てを
通過していることを示してます。
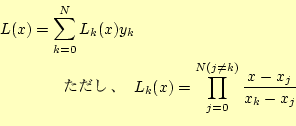 |
となります。
2.2 問題点
補間の点数が増えてくると、ラグランジュの補間には問題が生じます。具体例を図に示します。これを見ると分かるように、補間の関数が振動しています。ラグランジュの補間では、補間の点数が増えてくると大きな振動が発生して、もはや補間とは言えなくなります。ラグランジュの補間には常にこの問題が付きまといますので、データ点数が多い場合は使えません。ほかの補間を考える必要があります。ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成17年1月14日
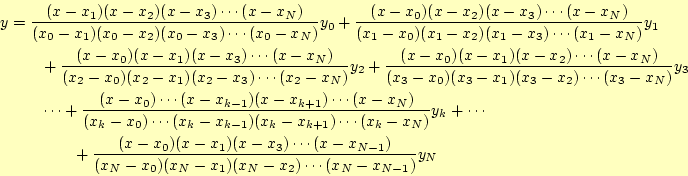
![\includegraphics[keepaspectratio,scale=0.5]{figure/lagrange_problem.eps}](img21.png)