3 スプライン補間
3.1 区分多項式
ラグランジュの補間は、データ点数が増えてくると関数が振動し問題が発生し ます。そこで、補間する領域をデータ間隔ここでは、通常よくつかわれる3次のスプライン補間を考えます。補間する関 数が3次関数を使うためそう呼ばれているのです。これ以降の説明は、文献 [1]を参考にしました。
補間をするデータは、先と同じように
![]() とします。そし
て、区間
とします。そし
て、区間
![]() で補間をする関数を
で補間をする関数を![]() とします。この様子を
図5に示します。
とします。この様子を
図5に示します。
3.2 係数が満たす式
3次のスプライン補間を考えるので、となります。この
これらの未知数は、4N個あります。従って、4N個の方程式が必要になります。 そのために、3次のスプライン補間に以下の条件を課します。
- 全てのデータ点を通る。各々の
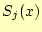 に対して両端での値が決まる
ため、2N個の方程式ができます。
に対して両端での値が決まる
ため、2N個の方程式ができます。
- 各々の区分補間式は、境界点の1次導関数は連続とする。これにより、 N-1個の方程式ができます。
- 各々の区分補間式は、境界点の2次導関数は連続とする。これにより、 N-1個の方程式ができます。
以上の条件を課すと方程式は4N-2個の方程式で表現できます。未知数は4N個な
ので、2個方程式が不足しています。この不足を補うために、いろいろな条件
が考えられますが、通常は両端![]() と
と![]() での2次導関数の値を0とします。
すなわち、
での2次導関数の値を0とします。
すなわち、
![]() です。
これを自然スプライン(natural spline)と言います。自然スプライン以外には、
両端の1次導関数の値を指定するものもあります。
です。
これを自然スプライン(natural spline)と言います。自然スプライン以外には、
両端の1次導関数の値を指定するものもあります。
これで全ての条件が決まりました。あとは、この条件に満たす連立方程式を求
めるだけです。まずは、2次導関数が区分関数の境界で等しいという条件から
です。![]() における2次導関数の値を
における2次導関数の値を![]() とします。すなわち、
とします。すなわち、
| (5) |
です。
| (6) |
となります。これから、
が、直ちに導けます。ここで、スプライン補間の係数、すなわち計算で求める べき
さらに2次導関数の計算から、
| (8) |
が導けます。この式から、
となります。これで、2次導関数の条件は終わりです。
つぎに、全てのデータ点上を通過する(最初の条件)という条件を考えます。ま ずは、区分の左端の点から、
が直ちに導けます。つぎに、区分の右端の点から
| (11) |
が導けます。式 (7),(9),(10)を用いると、
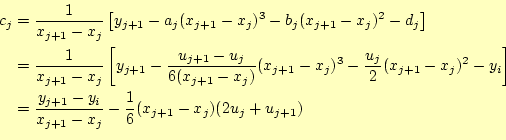 |
となります。
これで、![]() と
と![]() 、
、![]() 、
、![]() が
が![]() と
と![]() 、
、![]() で表せました。
で表せました。
![]() と
と![]() はデータ点なので、値はわかっています。したがって、
はデータ点なので、値はわかっています。したがって、![]() が
分かれば、補間に必要な係数が全て分かります。
が
分かれば、補間に必要な係数が全て分かります。
3.3 連立方程式
それでは、| (13) |
これと式(4)から、
| (14) |
となります。あとは、この式の
となります。この方程式は、
![]() を代入した連立1次方程式は、
を代入した連立1次方程式は、
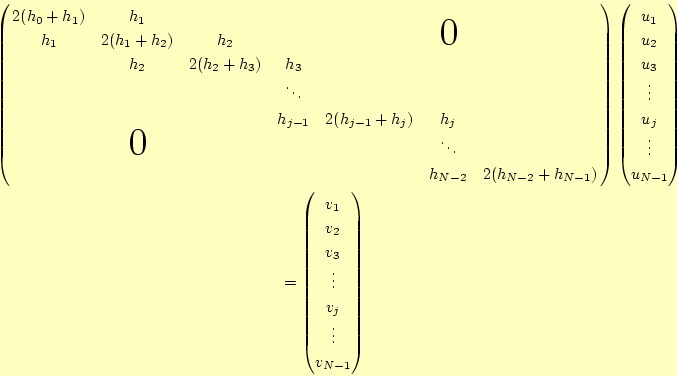 |
となります。ただし、
| (17) | ||||
![$\displaystyle =6\left[\frac{y_{j+1}-y_j}{h_j} -\frac{y_j-y_{j-1}}{h_{j-1}}\right]$](img60.png) |
(18) |
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成17年1月14日
![\includegraphics[keepaspectratio,scale=0.7]{figure/Spline.eps}](img25.png)
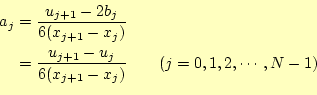
![$\displaystyle (x_{j+1}-x_j)u_j+2(x_{j+2}-x_j)u_{j+1}+(x_{j+2}-x_{j+1})u_{j+2}= ...
...\frac{y_{j+2}-y_{j+1}}{x_{j+2}-x_{j+1}} -\frac{y_{j+1}-y_j}{x_{j+1}-x_j}\right]$](img50.png)