4 実数解のニュートン法(Newton's method)

4.1 計算方法

関数$f(x)$のゼロ点$\alpha$に近い近似値$x_0$から出発する。そして、関数 $f(x)$上の点 $(x_0,f(x_0))$での接線が、x軸と交わる点を次の近似解$x_1$ とする。そして、次の接線がx軸と交わる点を次の近似解$x_2$とする。同じこ とを繰り返して $x_3,\,x_4,\cdots$を求める(図4)。こ の計算結果の数列 $(x_0,\,x_2,\,x_3,\,x_4,\cdots)$は初期値$x_0$が適当で あれば、真の解$\alpha$に収束する。

まずは、この数列の漸化式を求める。関数$f(x)$上の点 $(x_i,\,f(x_i))$の接 線を引き、それとx軸と交点$x_{i+1}$ である。まずは、$x_{i+1}$ を求める ことにする。点 $(x_i,\,f(x_i))$を通り、傾きが $f^\prime(x_i)$の直線の方 程式は、

$$y-f(x_i)=f^\prime(x_i)(x-x_i)$$ (4)

である。$y=0$の時の$x$の値が$x_{i+1}$にである。$x_{i+1}$は、

$$x_{i+1}=x_i-\frac{f(x_i)}{f^\prime(x_i)}$$ (5)

となる。$x_i$から$x_{i+1}$計算できる。これをニュートン法の漸化式と言う。 この漸化式を用いれば、次々と近似解を求めることができる。

計算の終了は、

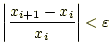$$\left\vert\frac{x_{i+1}-x_i}{x_i}\right\vert<\varepsilon$$ (6)

の条件を満たした場合とするのが一般的である。 $\varepsilon$は計算精度を 決める定数で、非常に小さな値である。これ以外にも計算の終了を決めること は可能である。必要に応じて、決めればよい。実際に式 (3)を計算した結果を図4に 示す。接線との交点が解に近づく様子がわかるであろう。

ニュートン法を使う上で必要な式は、式(5)のみで ある。計算に必要な式は分かったが、数列がどのように真の解$\alpha$に収束 するか考える。$x_{i+1}$ と真値$\alpha$の差の絶対値、ようするに誤差を 計算する。 $f(\alpha)=0$を忘れないで、テイラー展開を用いて、計算を進める と

$$\begin{aligned}\vert\alpha-x_{i+1}\vert &=\left\vert\alpha-x_i+... ...=\left\vert O\left((\alpha-x_i)^2\right)\right\vert \end{aligned}$$

となる。$i+1$番目の近似値は、$i$番目に比べて2乗で精度が良くなるのであ る。これを、二次収束と言い、非常に早く解に収束する。例えば、$10^{-3}$ の精度で近似解が得られているとすると、もう一回式 (5)を計算するだけで、$10^{-6}$程度の精度で近似 解が得られるということである。一次収束の2分法よりも、収束が早いことが 分かる。

ニュートン法の特徴をまとめると次のようになる。

長所

初期値が適当ならば、収束が非常に早い(図 6)。

短所

初期値が悪いと、収束しない(図7)。収束 しない場合があるので、反復回数の上限を決めておく必要がある。

図 4: $f(x)=x^3-3x^2+9x-8$の実数解をニュートン法で計算し、解の収 束の様子を示している。初期値$x_0=5$から始まり、接線とx軸の交点からよ り精度の高い回を求めている。

4.2 アルゴリズム

2分法同様、関数と計算を打ち切る条件はプログラム中に書くものとする。そ うすると、図5のようなニュートン法のフローチャー トが考えられる。

図 5: ニュートン法のフローチャート

4.3 プログラム

このプログラムを暗記する必要はない。テストでは、アルゴリズム上、重要な部分を虫食 いにして出題するつもりである(たぶん)。 =1

#include <stdio.h>
#include <math.h>
#define IMAX 50
double func(double x);
double dfunc(double x);

/*================================================================*/
/*       main function                                            */
/*================================================================*/
int main(){
  double eps=1e-15;         /* precision of calculation */
  double x[IMAX+10];
  char temp;
  int i=-1;

  printf("\ninitial value x0 = ");
  scanf("%lf%c", &x[0], &temp);
        
  do{
    i++;
    x[i+1]=x[i]-func(x[i])/dfunc(x[i]);

    printf("  %d\t%e\n", i, x[i+1]);

    if(fabs((x[i+1]-x[i])/x[i])<eps) break;
  }while(i<=IMAX);

  if(i>=IMAX){
    printf("\nnot converged !!! \n\n");
  }else{
    printf("\niteration = %dsolution x = %20.15f\n\n",i,x[i+1]);
  }

  return(0);
}

/*================================================================*/
/*       define function                                          */
/*================================================================*/
double func(double x){
  double y;

  y=x*x*x-3*x*x+9*x-8;

  return(y);
}

/*================================================================*/
/*       define derived function                                  */
/*================================================================*/
double dfunc(double x){
  double dydx;

  dydx=3*x*x-6*x+9;

  return(dydx);
}

ホームページ: Yamamoto's laboratory
著者: 山本昌志