5 複素数解のニュートン法(Newton's method)

5.1 計算方法

複素数解を求めるための漸化式は、テイラー展開から求めるのが簡単である。以降の議論 は、実数解でも成り立つが、複素数解を導くために、 4.1節と異なる説明を行う。実態は同じではある。

複素数ということで、 w(z)=0 の方程式の解を求める。その一つの解を、$z=\alpha$とする。即ち、 $w(\alpha)=0$である。そして、$i$番目 の近似解を$z_i$とする。ここから、$\Delta z$だけ移動したところの値は、

$$\begin{aligned}w(z_i+\Delta z)&=w(z_i) +w^\prime(z_i)\Delta z +... ... z^2 +\cdots\\ &\simeq w(z_i)+w^\prime(z_i)\Delta z \end{aligned}$$

となる。もし、 $w(z_i+\Delta z)=0$、即ち、 $\alpha=z_i+\Delta z$となるよ うに、$\Delta z$を選ぶことができたら、解の計算は簡単である。この場合、 式(8)の最後の式から、

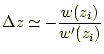$$\Delta z \simeq -\frac{w(z_i)}{w^\prime(z_i)}$$ (9)

となる。したがって、 $\alpha=z_i+\Delta z$から、次の近似解は

$$z_{i+1}=z_i-\frac{w(z_i)}{w^\prime(z_i)}$$ (10)

となる。グラフを用いて求めた、4.1節と同じ漸化式が 得られた。異なる説明であったが、内容はまったく同じであることを理解して欲しい。

ホームページ: Yamamoto's laboratory
著者: 山本昌志