2 連立一次方程式(反復法)

実用的なプログラムでは、非常に大きな連立方程式を計算しなくてはならない。数百万元 に及ぶことも珍しくない。これを、ガウス・ジョルダン法で 計算するの時間的にほとんど不可能である。そこで、これよりは格段に計算の速い方法が 用いられる。ここでは、その一つとして反復法を簡単に説明する。

当然ここでも、連立方程式

$$\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$$ (1)

を満たす $\boldsymbol{x}$を数値計算により、求めることになる。ここで、真の解 $\boldsymbol{x}$とする。

ここで、ある計算によりn回目で求められたものを $\boldsymbol{x}_n$とする。そして、計算回数を増やして、

$$\lim_{n\rightarrow\infty}\boldsymbol{x}_n=\boldsymbol{x}$$ (2)

になったとする。この様に計算回数を増やして、真の解に近づける方法を反復法という。

この様な方法は、行列 $\boldsymbol{A}$を $\boldsymbol{S}-\boldsymbol{T}$と分解するだけで、容易に作ることが できる。たとえば、

$$\boldsymbol{S}\boldsymbol{x}_{k+1}=\boldsymbol{T}\boldsymbol{x}_{k}+\boldsymbol{b}$$ (3)

とすればよい。ここで、 $\boldsymbol{x}_k$が $\boldsymbol{\alpha}$に収束するとする。すると、式 (3)と式(1)を比べれば、 $\boldsymbol{\alpha}$と $\boldsymbol{x}$は等しいことがわかる。すなわち、式(3)で元の方程式 (1)を表した場合、 $\boldsymbol{x}_k$が収束すれば、必ず真の解 $\boldsymbol{x}$に収束するのである。別の解に収束することはなく、真の解に収束するか、発散 するかのいずれかである。

2.1 ヤコビ法

計数行列 $\boldsymbol{A}$の対角行列を反復計算の行列 $\boldsymbol{S}$としたものがヤコビ(Jacobi)法で ある。ここでも、ヤコビは顔を出す。ヤコビ法では、係数行列を

$$\left[ \begin{array}{@{ }ccccc@{ }} a_{11} & a_{12} & a_{13} & ... ... & \ddots & \vdots a_{n1} & a_{n2} & a_{n3} & \ldots & 0 \end{array} \right]$$ (4)

と分解する。右辺第1項が行列 $\boldsymbol{S}$で第2項が $-\boldsymbol{T}$となる。 $\boldsymbol{x}_{k+1}$の解の 計算に必要な $\boldsymbol{S}$の逆行列は、それが対角行列なので、

$$\boldsymbol{S}^{-1}= \left[ \begin{array}{@{ }ccccc@{ }} a_{11}... ...vdots & \ddots & \vdots 0 & 0 & 0 & \ldots & a_{nn}^{-1} \end{array} \right]$$ (5)

と簡単である。k+1番目の近似解は、 $\boldsymbol{x}_{k+1}=\boldsymbol{S}^{-1}\left(\boldsymbol{b}+\boldsymbol{T}\boldsymbol{x}_k\right)$なので容易に求めるこ とができる。実際、k番目の解

$$x_1^{(k)}, x_2^{(k)}, x_3^{(k)}, \cdots, x_n^{(k)}$$

とすると、k+1番目の解は

$$\begin{aligned}&x_1^{(k+1)}=a_{11}^{-1}\left\{b_1-\left( a_{12}... ...k)}+ \cdots+a_{nn-1}x_{n-1}^{(k)}\right)\right\} \end{aligned}$$

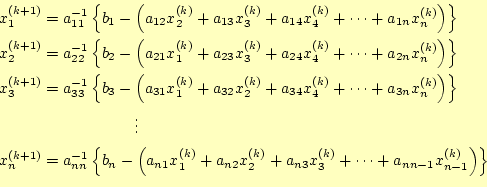と計算できる。これが、ヤコビ法である。

2.2 ガウス・ザイデル法

ヤコビ法の特徴では、 $\boldsymbol{x}^{(k+1)}$の近似値は、すべてその前の値 $\boldsymbol{x}^{(k)}$を 使うことにある。大きな行列を扱う場合、全ての $\boldsymbol{x}^{(k+1)}$と $\boldsymbol{x}^{(k)}$を記 憶する必要があり、大きなメモリーが必要となり問題が生じる。今では、個人で大きなメ モリーを使い計算することは許されるが、ちょっと前まではできるだけメモリーを節約し たプログラムを書かなくてはならなかった。

そこで、 $\boldsymbol{x}^{(k+1)}$の各成分の計算が終わると、それを直ちに使うことが考えば、 メモリーは半分で済む。即ち、$x_i^{k+1}$を計算するときに、

$$\begin{multline} x_i^{k+1}=a_{ii}^{-1}\left\{b_i-( a_{i1}x_1^{(k+1)}+a_{i2}x_2... ...+2}^{(k)}+a_{ii+3}x_{i+3}^{(k)}+\cdots+ a_{in}x_n^{(k)})\right\} \end{multline}$$

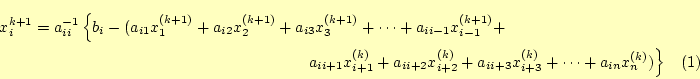
とするのである。実際の計算では、k+1番目の解は

$$\begin{aligned}&x_1^{(k+1)}=a_{11}^{-1}\left\{b_1-\left( a_{12}... ...)}+\cdots+a_{nn-1}x_{n-1}^{(k+1)}\right)\right\} \end{aligned}$$

と計算できる。これが、ガウス・ザイデル法である。

2.3 SOR法

ガウス・ザイデル法をもっと改善する方法がある。ガウス・ザイデル法の解の修正は、 $x_{k+1}-x_k$であったが、これをもっと大きなステップにしようというのである。通常 の場合、ガウス・ザイデル法では近似解はいつも同じ側にあり、単調に収束する。そのた め、修正を適当にすれば、もっと早く解に近づく。修正幅を、加速緩和乗数$\omega$を用 いて、 $\omega(x_{k+1}-x_k)$とする事が考えられた。これが、逐次加速緩和法(SOR法: Successive Over-Relaxation)である。

具体的な計算手順は、次のようにする。ここでは、ガウス・ザイデル法の式 (8)を用いて、得られた近似解を $\tilde{x}_i^{(k+1)}$としている。

$$\begin{aligned}&\tilde{x}_1^{(k+1)}=a_{11}^{-1}\left\{b_1-\left... ...mega\left(\tilde{x}_n^{(k+1)}-x_n^{(k)}\right) % \end{aligned}$$

これが、SOR法である。

ここで、問題なのが加速緩和係数$\omega$の値の選び方である。明らかに、それが1の場 合、ガウス・ザイデル法となりメリットは無い。また、1以下だと、ガウス・ザイデル法 よりも収束が遅い。ただし、ガウス・ザイデル法で収束しないような問題には使える。

従って、1以上の値にしたいわけであるが、余り大きくすると、発散するのは目に見えて いる。これについては、2を越えると発散することが分かっている。最適値となると、だ いたい1.9くらいが選ばれることが多い。

ホームページ: Yamamoto's laboratory
著者: 山本昌志