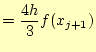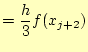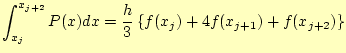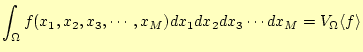4 数値積分
4.1 台形公式
定積分、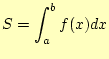 |
(12) |
の近似値を数値計算で求めることを考える。積分の計算は面積の計算であるから、図 2のように台形の面積の和で近似ができるであろう。積分の範 囲
となる。これが数値積分の台形公式である。なんのことはない、積分を台形の面積に置き 換えているだけである。
4.2 シンプソンの公式
台形公式の考え方は簡単であるが、精度はあまりよくない。そこで、よく似た考え方で精 度が良いシンプソンの公式を説明する。台形公式は、分割点の値を一次関数(直線)で近似 を行い積分を行った。要するに折れ線近似である。ここで、1次関数ではなく、高次の関 数で近似を行えばより精度が上がることは、直感的に分かる。
2次関数で近似を行うことを考える。2次関数で近似するためには、3点必要である。3つの
分点をそれぞれ、
![]() とする。そして、この2次関数を
とする。そして、この2次関数を![]() と
する。
と
する。![]() はラグランジュ補間に他ならないので、
はラグランジュ補間に他ならないので、
となる。図3に示すとおりである。
これを、区間
![]() で積分する。紙面の都合上、式
(15)の右辺を各項毎に積分を行う。まず、右辺第1項で
あるが、それは以下のようになる。
で積分する。紙面の都合上、式
(15)の右辺を各項毎に積分を行う。まず、右辺第1項で
あるが、それは以下のようになる。
同様に、第2,3項を計算すると
となる。以上より、近似した2次関数
となる。
これは、ある区間
![]() の積分で、その巾は
の積分で、その巾は![]() である。区間
である。区間![]() にわ
たっての積分
にわ
たっての積分![]() は、式(19)を足し合わせればよい。ただし、
は、式(19)を足し合わせればよい。ただし、
![]() と足し合わせる。
と足し合わせる。
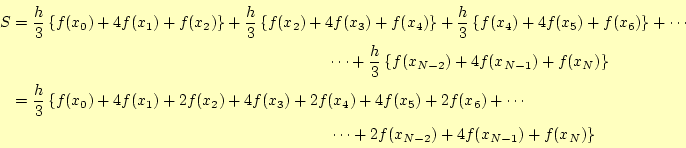 |
これが、シンプソンの公式と呼ばれるもので、先ほどの台形公式よりも精度が良い。精度 は、
この式から、分割数![]() は偶数でなくてはならないことがわかる。
は偶数でなくてはならないことがわかる。
4.3 モンテカルロ法
積分の境界が複雑な場合、乱数を使うモンテカルロ積分が適している。例えば、関数となる。ここで、
積分を計算するために、まずは体積である。これは体積の計算が容易な単純な形状の内部
に、領域![]() を包み込み、その内部にランダムに配置されたサンプル点の数を数えれ
ば良いのである。単純な形状内部に配置されたランダムな点の数を
を包み込み、その内部にランダムに配置されたサンプル点の数を数えれ
ば良いのである。単純な形状内部に配置されたランダムな点の数を![]() とする。そして、
その内部にある積分領域
とする。そして、
その内部にある積分領域![]() に含まれる点の数を
に含まれる点の数を
![]() とする。さらに、単純
な形状の体積を
とする。さらに、単純
な形状の体積を![]() 、領域
、領域![]() のそれを
のそれを
![]() とすると、
とすると、
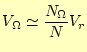 |
(20) |
の関係がある。右辺はコンピューターにより容易に計算できる。ランダムな点の数
残りは、体積内部の平均
![]() である。これも簡単で、領域
である。これも簡単で、領域![]() 内部
にあるサンプル点の平均より求めることができる。即ち、
内部
にあるサンプル点の平均より求めることができる。即ち、
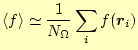 領域 領域 |
(21) |
となる。ここで、
以上より、モンテカルロ法を用いると、体積![]() と平均値
と平均値
![]() の近似値が
計算できることが分かる。従って、式(21)の近似値を求めることが
できる。
の近似値が
計算できることが分かる。従って、式(21)の近似値を求めることが
できる。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成17年3月1日
![\begin{equation*}\begin{aligned}T&=h\frac{f(a)+f(a+h)}{2}+ h\frac{f(a+h)+f(a+2h)...
...{2}\sum_{j=0}^{N-1}\left[f(a+jh)+f(a+(j+1)h)\right] \end{aligned}\end{equation*}](img59.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/trapezoidal.eps}](img60.png)
![\includegraphics[keepaspectratio, scale=1.0]{figure/simpson.eps}](img64.png)
![\begin{equation*}
% latex2html id marker 1716
\begin{aligned}\text{式(\ref{eq:si...
...i^2}{2}+2h^2\xi\right]_0^{2h} &=\frac{h}{3}f(x_j) \end{aligned}\end{equation*}](img66.png)