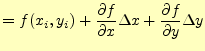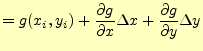8 より進んだ内容(ニュートン法)
4節では、ニュートン法により、実数解を求める方法を学習した。
そのとき、連立方程式や複素数解が求められると述べた。そこで、諸君の将来のために、
複素数解や連立方程式を求める方法を示しておく。内容は、実数解を求める方法とほとん
ど同じであるが、少しばかり概念を拡張する必要がある。いままでの学習内容を十分理解
していれば、これから述べることは分かるであろう。理解できないにしても、いずれは理
解できるものと期待している。内容が理解できなくても、なにか面白そうだと思ってもら
えれば、十分である。さあ、実数解が求められた者は、より難しい非線形方程式の近似解
を求めよう。
8.1 非線型方程式の複素数解
8.1.1 実数解の場合の復習
複素数に進む前に実数のニュートン法の復習を行う。4節ではでは、 図によるニュートン法の説明を行い、漸化式を示した。この方法は、直感的で分かりやす いが、複素数解や非線形連立方程式を考える場合は無理がある。図で示すことが出来るの は2次元までで、それ以上になると図に示すことが不可能であるからである。そこで、別 のアプローチから漸化式を導くことにする。異なった説明をしているようであるが、その 根本精神は全く同じで、- 解に近いところでは、直線で近似できる6。
それでは、漸化式を求めることにする。いつものように、![]() の方程式の解を
の方程式の解を
![]() とする。即ち、
とする。即ち、
![]() である。そして、
である。そして、![]() 番目の近似解を
番目の近似解を![]() とす
る。ここから、
とす
る。ここから、![]() だけ移動したところの値は、
だけ移動したところの値は、
となる。もし、
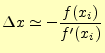 |
(16) |
となる。したがって、
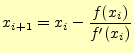 |
(17) |
となる。前回、図により求めた漸化式と同じである。異なる説明であったが、内容はまっ たく同じであることを理解して欲しい。
8.1.2 複素数解の場合
8.1.2.1 漸化式
実数とまったく同じ議論が、複素数でも成り立つ。ただし、複素関数で重要な特異点付近 では、この方法は使えない。テイラー級数ではなく、ローラン級数の実数とまったく同じ議論より、方程式
| (18) |
の近似解は、漸化式
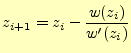 |
(19) |
より求めることができる。この式の算出は、先ほどの実数の場合と全く同じである。
前回とは異なり、実数の場合の漸化式をグラフを用いないで説明したのは、複素数に拡張 するためである。複素数のグラフは大変である。
8.1.2.2 プログラム作成のために
つい最近まで、FORTRANと違ってC言語では複素数をそのまま扱うことができなかった。こ れがC言語の弱点になっていたが、現在ではそれが克服された。FORTRAN同様に複素数もそ のまま扱えるのである。これは非常にありがたい。C言語で複素数を使うためには、教科書p.471に書かれているようにすればよい。すなわち、
#include <complex.h>とヘッダーファイルをインクルードし、変数の型を
float complex double complex long double complexのようにする。通常は、double complexを使うこと。
四則演算は特に気にすることもなく、普通に演算子(+,-,*,/)が使える。また、表1のような関数が用意されている。
| 関数名 | 倍精度 | 単精度 | 拡張倍精度 |
| 三角関数 | csin() | csinf() | csinl() |
| ccos() | ccosf() | ccosl() | |
| ctan() | ctanf() | ctanl() | |
| 逆三角関数 | casin() | casinf() | casinl() |
| cacos() | cacosf() | cacosl() | |
| catan() | catanf() | catanl() | |
| 双曲線関数 | csinh() | csinhf() | csinhl() |
| ccosh() | ccoshf() | ccoshl() | |
| ctanh() | ctanhf() | ctanhl() | |
| 逆双曲線関数 | casinh() | casinhf() | casinhl() |
| cacosh() | cacoshf() | cacoshl() | |
| catanh() | catanhf() | catanhl() | |
| 指数関数 | cexp() | cexpf() | cexpl() |
| 自然対数 | clog() | clogf() | clogl() |
| 絶対値 | cabs() | cabsf() | cabsl() |
| 平方根 | csqrt() | csqrtf() | csqrtl() |
| べき乗 | cpow() | cpowf() | cpowl() |
| 実部 | creal() | crealf() | creall() |
| 虚部 | cimag() | cimagf() | cimagl() |
| 偏角 | carg() | cargf() | cargl() |
| 複素共役 | conj() | conjf() | conjl() |
| リーマン球の射影 | cproj() | cprojf() | cprojl() |
8.2 非線型連立方程式の実数解(2元の場合)
前節では、ニュートン法による複素数の近似解を求める方法を示した。「非線型連 立方程式」の近似解が求めれれば、概ねニュートン法の学習は終わりである。ちょっと難 しいが、ニュートン法の学習の仕上げとして、「非線型連立方程式」の実数解を求める方 法を示す。非線型連立方程式の複素数解を求めることが残っているが、この講義では示さ ない。今までのことを理解していれば、その方法も直ぐに理解できるであろう。興味のあ る人、あるいは必要に迫られた人は、自分で計算方法を考えてみよう。8.2.1 非線型連立方程式とは
今まで、諸君は、「非線型の方程式」あるいは「線形の連立方程式」は解いたことがある。 例えば、前者は、| (20) |
のようなものである。後者の例は、
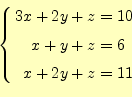 |
である。非線型方程式は未知数が2次以上のものをいい、連立方程式は未知数が2個以上の ものをいうのである。非線型とは、直線でないという意味である。未知数が2次以上のも の、例えば
複素数解まで含めると、非線型なn次方程式にはn個の解がある。線形な連立方程式、n元1次 方程式の場合、係数行列が特異でない限り、1個の解がある。では、非線形な連立方程式、n元 m次方程式の場合、複素数を含めた解の数はm個のように思えるが、正しいのだろうか?。 数学の先生に聞くと、正しいということである。
また、方程式の数と未知数の数は一致しなくてはならないのは、通常の連立方程式と同じ である。それらの数が同じでも、線形連立方程式では、係数行列の行列式がゼロの場合、 解は一意に決まらない。非線型の連立方程式の場合、これはどのような場合に対応するの だろうか?。私には、分からない。かなり難しく興味深い問題のように思えるが、ここで はそのことは考えないことにする。
8.2.2 非線型連立方程式の例
実例を使って、計算方法を示す。例として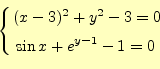 |
の近似解を求めることを考える。2元?次非線型連立方程式である。?次とは、いささかい い加減に書いているが、勘弁してもらいたい。無限次といってよいような気がするが自信 が無いので?マークを付けておく。
さて、この方程式の解であるが、それをグラフに示す。2元であればグラフに書くことが できるのである。以下の議論は、任意の元の方程式でも成り立つことは理解して欲しい。 これらの方程式をグラフに書くと図11のようになる。図中に示すよう に、点AとBに実数解があるのが分かるであろう。
初期値から出発して、解であるAやB点に近づく方法を考える。そこで、次のような関数を 考える。
| (23) | ||
| (24) |
もちろん、
いつものように、この非線型連立方程式の解を
![]() とする。当然、
とする。当然、
![]() かつ
かつ
![]() である。そして、
である。そして、![]() 番目の
近似解を
番目の
近似解を
![]() とする。ここから、
とする。ここから、
![]() だけ移動したところの
値は、
だけ移動したところの
値は、
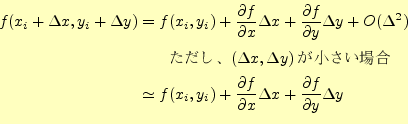 |
となる。
となる。
ここで、
![]() かつ
かつ
![]() と
なるように、
と
なるように、![]() と
と![]() を選ぶとする。このようにするためには、
を選ぶとする。このようにするためには、![]() と
と![]() はつぎの連立方程式を満たせばよい。式(26)と
(27)の左辺をゼロとおき式を整理すれば
はつぎの連立方程式を満たせばよい。式(26)と
(27)の左辺をゼロとおき式を整理すれば
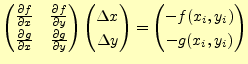 |
(28) |
となる。この連立方程式を解いて、
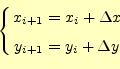 |
となる。これが、非線型連立方程式の漸化式である。
8.2.3 連立で無い場合とのアナロジー
以前の授業で示した方程式の実数解や複素数解を求めたのと同じようなことを、ここでも 行った。式も似ているし、考え方も同じである。以前は、- 解に近いところでは、直線で近似できる7。
- 解に近いところでは、平面で近似できる8。
8.3 非線型連立方程式の解(多元の場合)
前章では、2元の非線型連立方程式のニュートン法での計算方法を示した。ここでは、そ れを一般化する。ここで示す方法は、複素数解にも適用できる。N元の非線型連立方程式は、
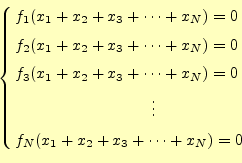 |
と書くことができる。未知数は、
| (31) |
とベクトルで表現する。すると、
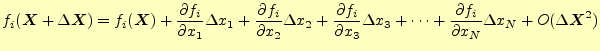 |
(32) |
となる。
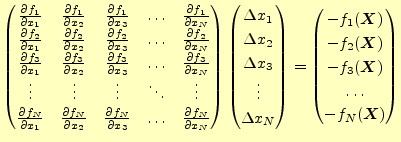 |
(33) |
の線形であるN元1次連立方程式が成り立つ。これを解いて、
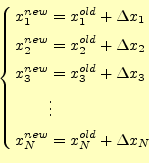 |
となる
非線型の連立方程式を線形の連立方程式で計算しているわけである。解きやすい式になっ た分、反復計算が必要となっている。
ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年6月24日
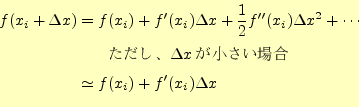
![\includegraphics[keepaspectratio, scale=1.0]{figure/nonlinear_eqs/ZeroPoint.eps}](img199.png)