4 ニュートン法(Newton's method)
4.1 計算方法
関数
実際にこの数列を計算するためには、漸化式が必要である。図の用にすると、関数![]() 上の点
上の点
![]() の接線を引き、それとx軸と交点
の接線を引き、それとx軸と交点![]() になる。まずは、
になる。まずは、
![]() を求めることにする。点
を求めることにする。点
![]() を通り、傾きが
を通り、傾きが
![]() の
直線の方程式は、
の
直線の方程式は、
| (8) |
である。図4より、
となる。これで、
計算の終了は、
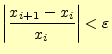 |
(10) |
の条件を満たした場合とするのが一般的である。
ニュートン法を使う上で必要な式は、式(9)のみである。計算
に必要な式は分かったが、数列がどのように真の解![]() に収束するか考える。
に収束するか考える。
![]() と真値
と真値![]() の差の絶対値、ようするに誤差を計算する。
の差の絶対値、ようするに誤差を計算する。
![]() を
忘れないで、テイラー展開を用いて、計算を進めると
を
忘れないで、テイラー展開を用いて、計算を進めると
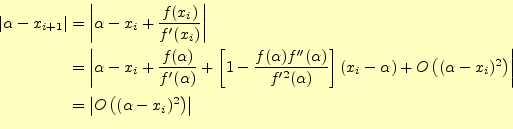 |
となる。
ニュートン法の特徴をまとめると次のようになる。
ニュートン法は複素数にも適用できる 。また、連立方程式にも容易に拡張できる。諸君
が学習してきた数は、自然数
![]() 整数
整数
![]() 有理数
有理数
![]() 無理
数
無理
数
![]() 複素数
複素数
![]() ベクトル
ベクトル
![]() 行列
行列
![]() と拡張されてきた。しかし、どのような数であれ、演算規則は非常に似通っていることは
今まで経験してきたとおりである。このことから、実数で成り立つ方法は、複素数や行列
にも成り立つことが予想できる。このように考えると、ニュートン法が連立方程式や複素
数に拡張できることも不思議ではない。
と拡張されてきた。しかし、どのような数であれ、演算規則は非常に似通っていることは
今まで経験してきたとおりである。このことから、実数で成り立つ方法は、複素数や行列
にも成り立つことが予想できる。このように考えると、ニュートン法が連立方程式や複素
数に拡張できることも不思議ではない。
これは少し高度な内容なので、8節におまけで載せておく。た ぶん、諸君の中の何人かは一瞬にして実数の近似解を求めるニュートン法を理解したと思 う。これまでの話が理解できた者は、8節を勉強することを勧 める。
4.2 フローチャート
二分法同様、関数と計算を打ち切る条件はプログラム中に書くものとする。そうすると、 図5のようなニュートン法のフローチャートが考えられる。ホームページ: Yamamoto's laboratory
著者: 山本昌志 Yamamoto Masashi
平成19年6月24日
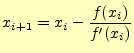
![\includegraphics[keepaspectratio, scale=0.7]{figure/function_solution/NewtonMethod.eps}](img116.png)
![\includegraphics[keepaspectratio, scale=0.8]{figure/flow_chart/flow_newton.eps}](img117.png)