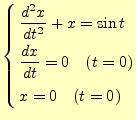5 使い方

5.1 高級電卓

まずは，円周率$\pi$の値を1000桁計算してみよう．入力ウインドウに

$$N[\pi,1000]$$

と入れて，[Shift]+[Enter]と計算を実行させてみよう．すると，1000桁の円 周率が打ち出されたはずである．ここで使ったコマンドはNで，N[計算式,桁数] と使う．

次に，簡単な分数の計算

$$\frac{987654321}{123456789}$$

を行う．計算の結果は分数で，正確な値が得られる．これは非常に驚くべきこ とで，CやFORTRANでは不可能である．正確な値ではなく，近似値が欲しい場合 は，

$$\texttt{N}\left[\frac{987654321}{123456789},1000\right]$$

とすればよい．これで，1000桁の近似値が得られる．

もう少し便利な電卓としての使い方は，

$$\begin{aligned}&\theta_1=\frac{\pi}{6};\\ &\theta_2=\frac{\pi}{... ...ta_2] -\texttt{Sin}[\theta_2]\texttt{Cos}[\theta_1] \end{aligned}$$

である．1行目と2行目のセミコロン`;`は，C言語の行の区切りではない．その行の計算結 果を出力しないという意味である．計算結果である3行目は出力させたいため，セミコロ ンが無い．3行目を

$$\texttt{Simplify}\left[\texttt{Sin}[\theta_1]\texttt{Cos}[\theta_2] -\texttt{Sin}[\theta_2]\texttt{Cos}[\theta_1]\right]$$

と書き換えれば，整理した結果が得られる．言うまでも無いが，3行目を

$$N\left[\texttt{Sin}[\theta_1]\texttt{Cos}[\theta_2] -\texttt{Sin}[\theta_2]\texttt{Cos}[\theta_1]\right]$$

と書き換えれば，近似値を求めることができる．

複素数の計算も問題なくできる．複素数が関係する最も美しい式

$$e^{i\pi}$$

を計算してみよう．ネピア数$e$と虚数単位$i$は，パレットから選択する必要がある．計 算の結果は，-1になるはずである．

線形代数の計算も簡単にできる．例えば，

$$\begin{aligned}&A=\{a_x,a_y,a_z\};\\ &B=\{b_x,b_y,b_z\};\\ &A.B\\ &\texttt{Cross}[A,B] \end{aligned}$$

でベクトルAとBの内積と外積が計算できる．固有値や固有ベクトル，行列式の計算もでき る．行列は，メニューの[入力] $\;\rightarrow\;$[表・行列・パレットの作成]を用いて 入力する．次の

$$\begin{aligned}&U= \begin{pmatrix}1 & 2 & 3 \\ 3 & 1 & 2 \\ 2 &... ...}[U]\\ &\texttt{Eigenvectors}[U]\\ &\texttt{Det}[U] \end{aligned}$$

のようにすれば行列の計算ができる．

5.2 微分と積分

5.2.1 微分

微分は，Dというコマンドを用いても，パレットから$\partial$を使っても可能である． 次の例のように，

$$\begin{aligned}&\texttt{D}[\texttt{Sin}[x],x]\\ &\partial_x\texttt{Sin}[x] \end{aligned}$$

できる．高次の微分は，

$$\texttt{D}[x^n,\{x,4\}]$$

のようにする． $\frac{\partial^3 \sin(x^2y)}{\partial x \partial^2y}$の ような偏微分は

$$\partial_{x,y,y}\texttt{Sin}[x^2\; y]$$

とすればよい．また，

$$\partial_xf[g[x]]$$

のようなこともできる．

5.2.2 積分

不定積分は，コマンドIntegrate，あるいはパレットから$\int$で可能である．たとえば，

$$\begin{aligned}&\texttt{Integrate}[x^n,x]\\ &\int x^ndx \end{aligned}$$

のようである．次のような複雑な積分

$$\int \sqrt{a+b\;\texttt{Cos}[c\;x]}dx$$

も可能である．結果は楕円関数になっている．積分記号も根号もパレットから選択する．

定積分は，

$$\begin{aligned}&\texttt{Integrate}[\frac{1}{1+x^2},\{x,0,1\}]\\ &\int_0^1\frac{1}{1+x^2}dx \end{aligned}$$

のようにしてできる．

数値積分は，

$$\texttt{NIntegrate}[(\texttt{Sin[x])}^2,\{\texttt{x},0,2\pi\}]$$

のように，NIntegrateコマンドを使う．

通常のプログラミング言語で計算できるのは，この数値積分だけである．Mathematicaで は不定積分や定積分の計算が可能である．これは，驚くべきことである．

5.3 グラフィックス

グラフィックの機能は豊富で，通常必要なグラフはほとんどMathematicaで書くことがで きる．C言語などの計算結果をMathematicaで出力することも行われており，グラフ作成が 非常に容易である．

5.3.1 2次元のグラフ

まずは，非常に単純な三角関数を例にして，グラフの書き方を示す．最初の例は，

$$\texttt{Plot}[\texttt{Sin}[x],\{x,0,2\pi\}]$$

である．

計算結果をグラフにする場合は，

$$\begin{aligned}&f[x\_]=\partial_x\texttt{Sin}[x^2];\\ &\texttt{Plot}[f[x],\{x,-2\pi,2\pi\}] \end{aligned}$$

のようにする．計算結果である微分を関数と定義して，プロットしている．関数を定義す るときは，変数の後に下線をつける．

媒介変数を使ったプロットは，

$$\texttt{ParametricPlot}[\{\texttt{Sin}[2t],\texttt{Sin}[3t]\}, \{t,0,2\pi\}]$$

のようにする．これは，リサジューの図形である．

グラフの形に不満があれば，オプションを使って，整形できる．論文などに計算結果のグ ラフを貼り付ける場合，オプションを駆使して，見栄えを整えるべきである．

5.3.2 3次元のグラフ

3次元グラフは

$$\texttt{Plot3D}[\frac{\texttt{Sin}[\sqrt{x^2+y^2}]}{\sqrt{x^2+y^2}}, \{x,-4\pi,4\pi\},\{y,-4\pi,4\pi\}]$$

と書けばよい．このままだと少し分かり難いので，オプションをつけるて分かり易くでき る．

$$\begin{aligned}&\texttt{Plot3D}[\frac{\texttt{Sin}[\sqrt{x^2+y^... ...,\\ &\quad \texttt{PlotPoints -> 100}\\ &\texttt{]} \end{aligned}$$

媒介変数による3次元プロットは，

$$\texttt{ParametricPlot3D[\{Cos[t]\;(3+Cos[u]), Sin[t]\;(3+Cos[u]), Sin[u]\}, \{t,0,2$\pi$\}, \{u,0,2$\pi$\}]}$$

のようにする．

その他，濃淡プロットや等高線プロットもできるので，各自，必要に応じて勉強するのが 良いだろう．

5.4 方程式

Mathematicaでの方程式の解き方は，いろいろある．ここでは，Sloveを用いた非線形方程 式と連立方程式，NDSolveを用いた微分方程式の計算方法を示す．

5.4.1 非線形方程式

普通，紙と鉛筆を用いて非線形方程式を解くことはできない．通常であれば，プログラム を作成して，ニュートン法等のアルゴリズムで方程式の近似解を得ることになる．

まず，簡単なところからはじめる．二次方程式は

$$\texttt{Solve[a x$^2$\ + b x + c == 0,x]}$$

とする．二次方程式の解析解が得られるはずである．このように解析解がない場合は， ニュートン法を使うことになる．例えば $\cos x-x=0$のような方程式は

$$\texttt{FindRoot[Cos[x]-x== 0,\{x,0.5\}]}$$

とする．最初に式を書き，次に変数とその初期値をあたえる．これでニュートン法により 計算できる．

5.4.2 連立方程式

連立方程式は，Solveコマンドで計算できる．例えば，

$$\texttt{Solve[\{x+2y==3,4x+5y==6\},\{x,y\}]}$$

のようにする．これは，

• Solveは，方程式を解くためのコマンドである．引数は，以下の通りで ある．
  • 第1引数は，解くべき方程式である．これが複数ある場合，括弧 {}で囲んで，リストにする．
  • 第2引数は，解を求めるべき変数である．この場合も，複数ある場合，括弧 {}で囲んで，リストにする．

となっている．

5.4.3 常微分方程式

次は，常微分方程式の計算方法を示す．解くべき常微分方程式は

$$\left\{ \begin{aligned}&\frac{d^2x}{dt^2}+x=\sin t\\ &\frac{dx}{dt}=0\quad(t=0)\\ &x=0\quad(t=0) \end{aligned} \right.$$

とする．これは，強制振動の方程式である．この系の固有振動数は， $\omega_0=1$である． そして，外力の角振動数も$\omega=1$となって，共振している．

Mathematicaで数値計算して解くには，

$$\begin{aligned}&\texttt{result=NDSolve[}\\ &\qquad\texttt{\{x''... ...x[t] /. result;}\\ &\texttt{Plot[f[t],\{t,0,500\}]} \end{aligned}$$

とする．ここで，使われているコマンドの内容は，次の通りである．

• NDSolveコマンドで，微分方程式を数値計算する．計算された結果は， solveに代入される．このコマンドの引数は，
  • 第1引数は，解くべき方程式である．初期条件も入れて，連立微分方程式 の形にし，リストで記述する．
  • 第2引数は解くべき関数である．
  • 第3引数は，独立変数とその範囲をリストで記述する．
  である．
• 次にコマンド/.で，計算結果resultの関数x[t]を f[t]に置き換えている．
• Plotコマンドで，計算結果をグラフにしている．このコマンドの引数は，
  • 第1引数は，プロットする関数である．
  • 第2引数は，関数の独立変数とプロットの範囲である．
  である．

さあ，実行してみよう．どのような解が得られるか?．次に，外力の振動数を少し変化さ せた場合どのようになるか，調べよ．

先ほどのコマンドは，パレットを用いて

$$\begin{aligned}&\texttt{result=NDSolve[}\\ &\qquad\texttt{\{$\p... ...x[t] /. result;}\\ &\texttt{Plot[f[t],\{t,0,500\}]} \end{aligned}$$

としても良い．この方が，式の内容が分かりやすい．パレットを使って，数学で使う表記 にした方が，ミスが少ないし，後で内容を再考しやすい．

C言語などで，プログラムを作成して計算することを考えると，いかにMathematicaが簡単 かが分かるであろう．

5.5 音

任意の波形の音を出すこともできる．例えば，音階のラの音--440[Hz]--は

$$\begin{aligned}&\texttt{ra = 440;}\\ &\texttt{Play[Sin[2 $\pi$\ ra t],\{t, 0, 5\}]} \end{aligned}$$

とする．これで，440[Hz]の$\sin$波の音が5秒間鳴る．

[練習1]

440[Hz]と441[Hz]の音を重ね合わせて，1[Hz]のうなりを聞いてみよ う．

5.6 その他

Mathematicaでは画像処理もできる．ここでは，割愛するので，興味がある人は，自分で 学習して欲しい．
ホームページ: Yamamoto's laboratory
著者: 山本昌志