ベクトルラプラシアンは、ベクトル解析の恒等式
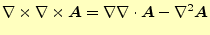 |
(17) |
に表れる。この式の右辺第2項がベクトルラプラス演算子(ベクトルラプラシアン)である。
従って、ベクトルラプラス演算子は、
から計算できる。右辺は、勾配と発散、回転からなる。式
(1),(2),(3)を用いて計算することになるが、
これには多くの計算が必要である。時間があるときに、Mathematicaのような数式処理シ
ステムを使って、計算することにする。
式(18)に、式
(4),(5),(6)を代
入して計算する。
カーテシアン座標形は、すべての軸が同じ形をしている。従って、他の軸のベクトルラプ
ラス演算子は、
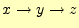 とサイクリックに記号を入れ替えるこ
とにより容易に求められる。まとめると、カーテシアン座標系のベクトルラプラス演算子
は、
とサイクリックに記号を入れ替えるこ
とにより容易に求められる。まとめると、カーテシアン座標系のベクトルラプラス演算子
は、
となる。実に、単純である。
円柱座標系も同じようにして、ベクトルラプラス演算子を求めることができる。式
(7),(8),
(9)を式(18)に代入
すればよい。
次に、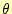 方向であるが、カーテシアン座標系みたいに添え字を入れ替えるだけでは
すまない。式(21)の途中までは、添え字が異な
るだけで同じである。異なる部分から計算を進めると、以下のようになる。
方向であるが、カーテシアン座標系みたいに添え字を入れ替えるだけでは
すまない。式(21)の途中までは、添え字が異な
るだけで同じである。異なる部分から計算を進めると、以下のようになる。
最後に、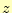 方向である。同じように計算をする。
方向である。同じように計算をする。
これまでの結果をまとめると、円柱座標系のベクトルラプラス演算子は、次のようになる。
極座標系のベクトルラプラス演算子の計算は、円柱座標よりもさらに大変である。ここで
は結果を載せることにとどめる。簡単に計算する方法が分かれば、これを改訂して載せる。
極座標
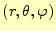 のベクトルラプラス演算子は、次のようになる。
のベクトルラプラス演算子は、次のようになる。
ホームページ: Yamamoto's laboratory
著者: 山本昌志
Yamamoto Masashi
平成20年3月24日
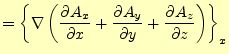
![$\displaystyle \quad\qquad -\left\{\nabla\times\left[ \left( \if 11 \frac{\parti...
...ac{\partial^{1} A_x}{\partial y^{1}}\fi \right)\boldsymbol{k} \right]\right\}_x$](img40.png)
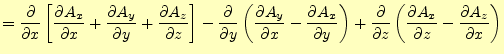
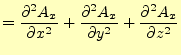
![]() とサイクリックに記号を入れ替えるこ
とにより容易に求められる。まとめると、カーテシアン座標系のベクトルラプラス演算子
は、
とサイクリックに記号を入れ替えるこ
とにより容易に求められる。まとめると、カーテシアン座標系のベクトルラプラス演算子
は、
![$\displaystyle = \frac{1}{r} \if 11 \frac{\partial }{\partial \theta} \else \fra...
...{\partial \theta} \else \frac{\partial^{1} A_r}{\partial \theta^{1}}\fi \right]$](img57.png)
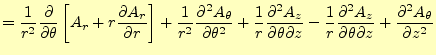
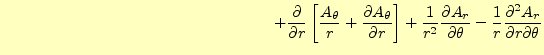
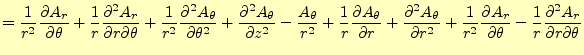
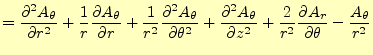
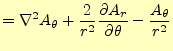
![]() のベクトルラプラス演算子は、次のようになる。
のベクトルラプラス演算子は、次のようになる。