3 実際の計算方法

3.1 ガウス・ザイデル法

境界条件，境界でのポテンシャルの値を決めることで，方程式と未知数の数が一致するこ とは前に示したとおりである．したがって，連立方程式を解けば，格子点のポテンシャル は分かることになる．しかし，実際問題この方程式を作るのが大変である．未知数のポテ ンシャルは，分かりやすくするために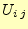$U_{i\,j}$と行列で表示したが，実際に連立方程式 を解く場合，未知数はベクトルになる．この式を書くのは大変厄介である．本当に大 変かどうかは，諸君が実際に，係数行列と同次項を求めてみれば分かる．

そこで，次のお手軽な方法で連立方程式を解くことにする．この方法は，連立方程式の係 数行列や同次項を求める必要がなく，プログラムは非常に簡単になる．

1. 外周の境界上の格子点のポテンシャルの値を$U_{i\,j}$に代入する．こ の値は，これ以降，ずっと一定とする．
2. 電極の内部の格子点のポテンシャルの値を$U_{i\,j}$を代入する．この 値も，これ以降，ずっと一定とする．
3. 計算すべき内部の格子点のポテンシャルを，

   $$U_{i\,j}=\frac{1}{4} \left[U_{i+1\,j}+U_{i-1\,j}+U_{i\,j+1}+U_{i\,j-1}\right]$$ (10)

   
   
   に従い計算する．
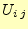4. $U_{i\,j}$が収束するまで，繰り返し，式 (10)を計算する．

実際，この方法で無限の回数ループ処理をすれば，対角優位行列なので真の解に収束する はずである．このように，反復により解に収束させる方法を反復法 と言う．とくに，ここで示した方法をガウス・ザイデル法 という．以前学習したしたように，SOR法 の方が収束が早いが，ここではプログラムが簡単なガウス・ザイデル法で計算するのが良 いであろう．

3.2 内部電極の決め方

ある注目している格子点が，ポテンシャルが固定されている内部電極の内側にあるか否か 判断しなくてはならない．内部にあるとそれは固定点で，先に示したガウス・ザイデル法 で値を変えてはならない．一方，外部だと境界でない限り，ガウス・ザイデル方で収束す るまで，計算を繰り返すことになる．そのようなことから，電極内部にあるか否かは予め 判断する必要がある．その判断は簡単である．格子点と電極中心の距離と電極半径を比べ れば良いのである．

3.3 固定及び境界点の計算を省く方法

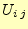固定電極内部の点や外部の境界の格子点では，ガウスザイデル方で計算する必要がない． それを計算しないようにプログラムを書かなくてはならない．境界の計算を省くのは簡単 である．境界の格子点のポテンシャルは， $i=0, i=N_x, j=0, j=N_y$の場合である．この 場合，ガウス・ザイデル法で式(10)の$U_{i\,j}$を計算し なければ良いのである．

次に，電極内部の点であるが，これは予め目印を付ければ良い．例えば，整数型の配列を 用意して，その値が1の場合は，電極の内部と目印をしておく．1以外の時，式 (10)の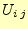$U_{i\,j}$を計算する．

以上をまとめると，連立方程式を解く場合には，次のようなループとすれば良いであろう．

	for(k=1; k<=ガウス・ザイデル法の計算回数;k++){
	  for(j=1; j<= x方向の分割数-1 ; j++){
	    for(i=1; i<= y方向の分割数-1 ;i++){
	      if(フラグ[i][j] != 1){
	        u[i][j]=0.25*(u[i][j-1]+u[i][j+1]+u[i-1][j]+u[i+1][j]);
	      }
	    }
	  }
	}

このループを図7に示す．先のループがどのように計算されるか，よ く考えよ．

図 7: 計算する格子点と順序

ホームページ: Yamamoto's laboratory
著者: 山本昌志